The waves and the wind. Calculation of wave characteristics
Calculation of wave characteristics
We were asked to create a calculator for the "calculation of the wave height and intervals between waves (frequency)?".
Intuition suggests that there is some relationship between the force of the wind and waves. Since I don't know much about wave theory, I've got to study it.
The result of my study is a calculator below, along with my thoughts on the subject. The calculator does not calculate, or more precisely, does not predict the height of the waves - is a separate issue covered here - The waves and the wind. Wave height statistical forecasting.
Theory
Obviously, the waves on the sea can not be described by a single sine wave, as they are formed as a result of imposing a plurality of waves with different periods and phases. For example, look at the picture below, which shows the wave resulting from the imposition of three different sine waves.

Source: "Wave disp" by Kraaiennest - Own work. Licensed under GFDL via Wikimedia Commons - http://commons.wikimedia.org/wiki/File:Wave_disp.gif#mediaviewer/File:Wave_disp.gif
Therefore, for analysis of the sea state, energy spectrum is usually built, energy units lotted on the Y-axis, and frequency on the X-axis, thus obtaining energy density - the amount of energy carried by waves with a corresponding frequency range. As it turned out, under the wind's influence, the shape of the energy spectrum is changed. The stronger the wind, the more strongly peak in the spectrum expressed - waves of certain frequencies carrying the most energy. In the picture below have drawn its approximate look as best I could.
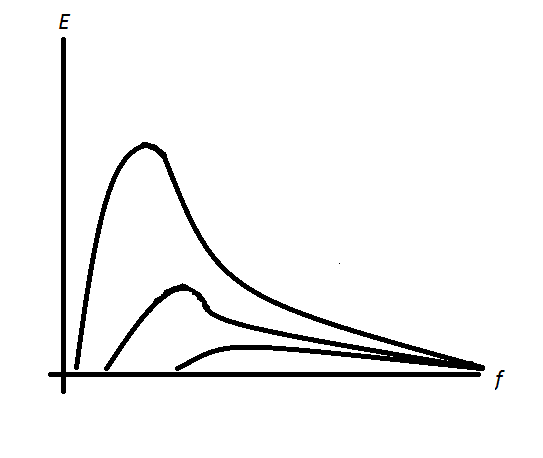
The frequencies where a peak is observed are called dominant. Accordingly, you can make your life easier and calculate the waves' characteristics only for the dominant frequency. The practice has shown that it will be enough to give a good approximation to reality.
What concerns waves' characteristics, the linear wave theory comes to help, namely, the calculation of gravitational waves in the linearized approximation. To make it clearer what I mean, let's give some definitions further from
wikipedia:
Capillary waves —the name of various waves generated at the interface between a liquid and a gas or liquid and liquid. The lower part of waves is called trough, higher— crest.
Gravity waves on the water — kind of waves on the surface of the liquid in which the force returning the deformed surface of the liquid to a state of balance are simply the force of gravity related to the height difference of crests and troughs in the gravitational field.
Wave dispersion — in the wave theory, the difference in phase velocities of linear waves according to their frequency. That is, different wavelengths (respectively of different frequency) have different speeds in an environment that has clearly demonstrated experience with the refraction of light in a prism. This is important for further discussion
Wavenumber — is the 2π radians to the wavelength ratio: .Wavenumber can be represented as the difference in wave phase (in radians) at the same time in the spatial points at a distance per unit length (one meter) or a number of spatial periods (crest) of waves arriving at 2π meters.
Using the definition of the wavenumber, we can write the following formula:
Wavelength
Phase velocity (crest velocity )
Wave period(expressed in terms of angular frequency)
The picture to draw attention - кred dot shows the phase velocity, green - the group velocity (the velocity of the wave packet)

Source: "Wave group" by Kraaiennest - Own work. Licensed under GFDL via Wikimedia Commons - http://commons.wikimedia.org/wiki/File:Wave_group.gif#mediaviewer/File:Wave_group.gif
The dispersion law
The key element in the calculation of the characteristics of the wave is the concept of the dispersion law or dispersion relation (ratio)
The dispersion law or dispersion equation(ratio) in the wave theory - is the relationship of frequency and wave vector (wave number).
In general terms, this relationship is written as
.
This ratio of water derived in the linear wave theory for the so-called free surface, i.e., the surface of the liquid, not limited to the walls of the vessel or bed, and looks as follows:
,
where
g - acceleration of free fall,
k - wave number,
tanh - hyperbolic tangent,
h - distance from the liquid surface to the bottom.
It is possible to simplify further the formula based on the graph of the hyperbolic tangent. Note that for kh, tends to zero, the hyperbolic tangent can be approximated by its argument, i.e., kh value, and if kh, tends to infinity, the hyperbolic tangent kh tends to one. The latter case, obviously, relates to a very great depth. Is it possible to evaluate how they need to be big? If you take the hyperbolic tangent of pi, its value is approximately equal to 0.9964, which is already quite close to one (the number Pi is taken for the formula's convenience). Then
.
To calculate the characteristics of the wave, water can be considered as deep if the depth is more than at least half the wavelength, and in most places of the world ocean, this condition is met.
In general, based on the hyperbolic tangent graph, the following classification of waves for the relative depth is used (ratio of depth to wavelength).
1. Waves in deep water
The depth is more than half of wavelength, the hyperbolic tangent approximates by one
2. Waves on the transitional depths
The depth from one-twentieth to one-half wavelength, the hyperbolic tangent can not be approximated
3. Waves in shallow water
The depth less than one-twentieth of the wavelength, the hyperbolic tangent approximated by its argument
Consider the ratio for these cases:
The case of shallow water
The equation takes the form
,
whence
The group velocity for the case of shallow water
According to the theory, in shallow water, the wave does not have to have dispersion because the phase velocity is independent of frequency. However, we must remember that nonlinear effects in shallow water are beginning to work associated with the increase in wave amplitude. It starts happening when the amplitude of the wave is comparable to its length. One of the characteristic effects of this mode is the appearance of fractures on the wave tops. Also, there is a possibility of wave breaking - a well-known surf. These effects are not yet amenable to precise analytic calculation.
Transitional depths case
The equation is not simplified, and then
The group velocity for transitional depths
Note that the equation of the wavelength is transcendental, and find its solution should be found numerically. For example, usingFixed-point iteration method
Deep water case
The equation takes the form
,
whence
The group velocity in the deep water case
So, by measuring the period of a wave with sufficient accuracy, we can calculate the phase velocity, group velocity, and wavelength. And the measurement of the wave period can be made, for example, by timing the passage time of wave crests with a stopwatch, i.e., the period - this is the most reasonable thing that can be measured without special instruments. If you are somewhere near the coast - it is necessary to know the depth. If the depth is obviously big, you can use formulas for the deep water, in which the depth, as a parameter, is not included. Since we have a computer processing power at hand, the calculator does not use the simplified formula, finding wavelength by iteration method (method will converge, as the function's derivative is less than one).
Now, back to the wind. The wind, constantly blowing in one direction, generates the waves by transmitting its energy to them.
And quite obvious, to transmit energy to waves, the wind should blow faster, or at least at a rate equal to the wave's phase velocity.
Here comes a fully developed sea formulation. Fully developed sea - wave, which achieved maximal values at a given wind. The wave is in equilibrium concerning energy - as much energy is transmitted, as much goes into the motion. Not every wave reaches such a state, as it's required for the wind to constantly blow over the entire surface, which the wave passes for some time. And the stronger the wind, the more time and distance required for the formation of such a wave. When it's formed, it will certainly catch up with the phase velocity of the wind speed.
Comments