Earth Radius by Latitude (WGS 84)
This online calculator calculates Earth radius at given latitude using WGS 84 reference ellipsoid
The calculator below calculates Earth radius at a given latitude. In fact, of course, it calculates the radius of WGS 84 reference ellipsoid at a given latitude, and if you want some theory recap, you can find it below the calculator.
Earth radius
Since the Earth is flattened at the poles and bulges at the equator, geodesy represents Earth's shape with an oblate spheroid. The oblate spheroid, or oblate ellipsoid, is an ellipsoid of revolution obtained by rotating an ellipse about its shorter axis. It is the regular geometric shape that most nearly approximates the shape of the Earth. A spheroid describing the Earth's figure or other celestial body is called a reference ellipsoid. The reference ellipsoid for Earth is called an Earth ellipsoid.
Earth's physical surface is irregular. It can be approximated by the geoid, which was an important concept for almost two hundred years of history of geodesy and geophysics. According to Gauss, who first described it, it is the "mathematical figure of Earth", a smooth but highly irregular surface whose shape results from the uneven distribution of mass within and on Earth's surface. The geoid surface is irregular but considerably smoother than Earth's physical surface.
Because of their relative simplicity, reference ellipsoids are used as a preferred surface on which geodetic network computations are performed, and point coordinates such as latitude, longitude, and elevation are defined. Currently, the most common reference ellipsoid used, and that used in the context of the Global Positioning System is the one defined by WGS 84.
Two quantities uniquely define an ellipsoid of revolution. Several conventions for expressing the two quantities are used in geodesy, but they are all equivalent to and convertible with each other:
- Equatorial radius a (called semi-major axis), and polar radius b (called semi-minor axis);
- a and eccentricity e;
- a and flattening f.
WGS 84 defines ellipsoid parameters as:
Semi-major axis a = 6378137.0 meters
Semi-minor axis b = 6356752.3142 meters
Point on the ellipsoid surface can be defined by the parametric curve equation
Radius can be found using the Pythagorean theorem
However, the problem is that the angle t from the example above is the geocentric latitude, and coordinates provided in geodetic datum, like WGS 84, are geodetic. Geodetic latitude is determined by the angle between the equatorial plane and normal to the ellipsoid. In contrast, the geocentric latitude is determined by the angle between the equatorial plane and line joining the point to the ellipsoid center (see figure).
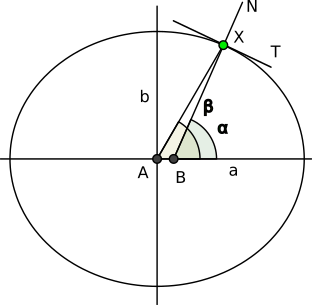
So, to find the radius, we need to relate geodetic latitude to geocentric latitude
.
Let's start from tangent of our curve, which can be obtained by differentiating curve equation.
This is the vector that points along the curve (along T-line on the figure).
We can rotate it clockwise 90 degrees and get normal vector
which points along N-line.
Parameter t is our . The slope of normal vector is also tangent of the angle
. Thus
or
Using the relations between tangent and cosine
and between tangent and sine
,
we can rewrite formula for radius as
and replace tangent of with tangent of
expression
Then, we can simplify it a bit
And, finally, get the formula from wikipedia
The calculator above uses this formula.
Comments