Spherical cap and spherical segment
This calculator computes volume and surface area of spherical cap and spherical segment

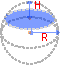
A spherical cap is the region of a sphere that lies above (or below) a given plane. If the plane passes through the center of the sphere, the cap is called a hemisphere.
Formulae:
- lateral surface area
- base surface area
- volume

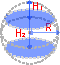
A spherical segment is the solid defined by cutting a sphere with a pair of parallel planes. It can be thought of as a spherical cap with the top truncated, and so it corresponds to a spherical frustum.
Formulae:
- lateral surface area
- volume
URL copied to clipboard
Similar calculators
Engineering Geometry hemisphere lateral surface area Math spherical cap spherical segment surface area volume
PLANETCALC, Spherical cap and spherical segment
Comments