PLANETCALC Online calculators

Login
StudyMathGeometry

Spherical cap and spherical segment

This calculator computes volume and surface area of spherical cap and spherical segment

This page exists due to the efforts of the following people:

A

Anton

Timur

Timur

Created: 2011-07-16 07:23:47, Last updated: 2021-02-25 08:57:21
Creative Commons Attribution/Share-Alike License 3.0 (Unported)

This content is licensed under Creative Commons Attribution/Share-Alike License 3.0 (Unported). That means you may freely redistribute or modify this content under the same license conditions and must attribute the original author by placing a hyperlink from your site to this work https://planetcalc.com/283/. Also, please do not modify any references to the original work (if any) contained in this content.

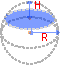
Spherical cap
Spherical cap

Spherical cap
Spherical cap



A spherical cap is the region of a sphere that lies above (or below) a given plane. If the plane passes through the center of the sphere, the cap is called a hemisphere.

Formulae:
S_{lateral}=2 \pi R H - lateral surface area
S_{base}=\pi{H}(2R-H) - base surface area
V=\pi H^2(R- \frac{1} {3} H) - volume

PLANETCALC, Spherical cap

Spherical cap

Digits after the decimal point: 5
Lateral surface area
 
Base surface area
 
Surface area
 
Volume
 



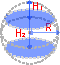
spherical segment
spherical segment



spherical segment
spherical segment

A spherical segment is the solid defined by cutting a sphere with a pair of parallel planes. It can be thought of as a spherical cap with the top truncated, and so it corresponds to a spherical frustum.

Formulae:
S_{lateral}=2 \pi R (H_2-H_1) - lateral surface area
V = \pi \left[ H_2^2 \left( R - \frac{1} {3} H_2 \right) - H_1^2 \left( R - \frac{1} {3} H_1 \right) \right] - volume

PLANETCALC, Spherical segment

Spherical segment

Digits after the decimal point: 5
Lateral surface area
 
Surface area
 
Volume
 

URL copied to clipboard

Similar calculators

 Engineering Geometry hemisphere lateral surface area Math spherical cap spherical segment surface area volume
PLANETCALC, Spherical cap and spherical segment
Anton2021-02-25 08:57:21

Comments