Secant method
The secant method is a root-finding algorithm that uses a succession of roots of secant lines to better approximate a root of a function f. A brief secant method description can be found below the calculator
Secant method
The secant method can be thought of as a finite difference approximation of Newton's method, where a derivative is replaced by a secant line.
We use the root of a secant line (the value of x such that y=0) as a root approximation for function f.
Suppose we have starting values x0 and x1, with function values f(x0) and f(x1).
The secant line has the equation
Hence, the root of secant line (where у=0) is
This is a recurrence relation for the secant method. A graphical interpretation can be seen below.
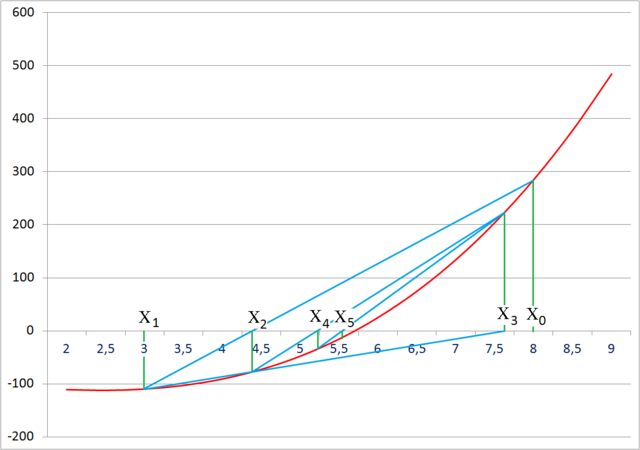
The secant method does not require that the root remains bracketed like the bisection method does (see below), and hence it does not always converge.
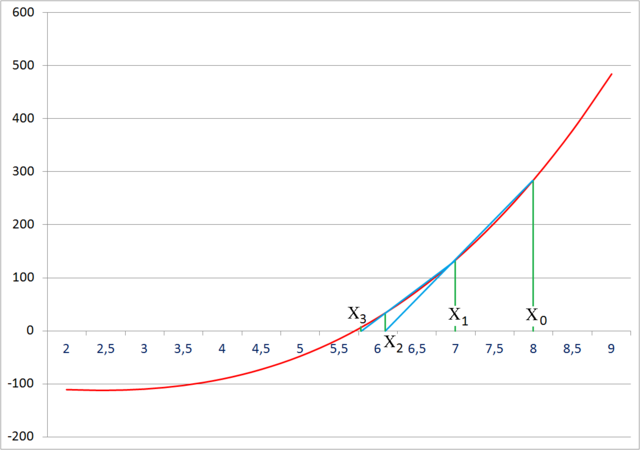
As can be seen from the recurrence relation, the secant method requires two initial values, x0 and x1, which should ideally be chosen to lie close to the root.
The tolerance condition can be either:
— function value is less than ε.
— the difference between two subsequent хk is less than ε.
More: Secant method
Comments