Distance through the Earth
This calculator calculates the distance from one point on the Earth to another point, going through the Earth, instead of going across the surface.
If you want to measure the distance from one point on the Earth to another, you should use the great-circle or orthodromic distance formula. We even have two calculators for this: the one which uses haversine formula, and the another one, which uses Vincenty formula.
However, what if you want to know the distance between two points on the Earth through the Earth, not across the surface? As it turns out, the problem is relatively simple, except for a couple of gotchas. The calculator below finds the distance between two points through the Earth, and the derivation of the formula with all gotchas can be found below the calculator.
Distance through the Earth
Ok, we have two points on the Earth's surface, defined by their latitude and longitude, and we want to know the distance between them going "through" the Earth instead of around it. Technically, we have spherical coordinates of each point in three-dimensional space because we know the Earth's radius, inclination angle (latitude), and azimuth angle (longitude). If we convert these to cartesian coordinates, with x, y, z in three-dimensional space, we can easily find the distance using the well-known Euclidean distance formula:
So, let's define our Cartesian coordinate system. Origin will be the center of the Earth. The x-axis will point to zero meridian intersection with the equator plane. The y-axis will point to 90 degrees west meridian intersection with equator plane z-axis will point to the North.
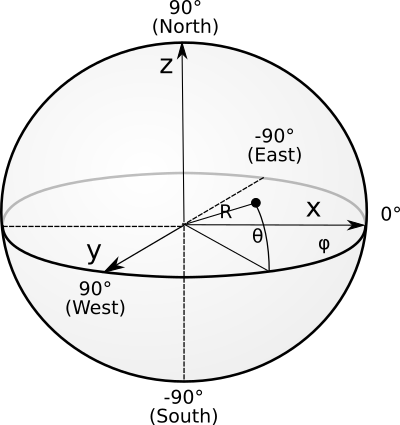
is our longitude,
is our latitude.
Cartesian coordinates can be obtained from spherical coordinates using the following relations:
We're almost done, but we still need to consider a couple of factors, which arise because, in geodesy, the Earth is approximated with oblate spheroid or ellipsoid of revolution. So, when we talk about coordinates, we talk about coordinates on the surface of reference ellipsoid used in the geodetic datum, in this case, WGS 84 (hence, the distance is also measured between two points of reference ellipsoid). The factors are:
Since the Earth is flattened at the poles and bulges at the equator, the Earth radius is not constant and depends on the latitude of the point. Thus, we need to compute it for both points, which can be done with this calculator.
WGS 84 latitude of a point is geodetic latitude, determined by the angle between the equatorial plane and normal to the ellipsoid instead of geocentric latitude, which is determined by the angle between the equatorial plane and line joining the point to the center of the ellipsoid. Since our cartesian system's origin is the center of the Earth, we need to convert geodetic latitude to geocentric latitude for both points.
We account for those using these formulas:
,
where is geocentric latitude,
is geodetic latitude,
- semi-major axis of the ellipsoid,
- semi-minor axis of the ellipsoid.
To summarize, to calculate the distance, we should do the following:
- Calculate Earth radius at each point
- Calculate geocentric latitude at each point
- Convert spherical coordinates of each point to cartesian coordinates, from calculated radius, geocentric latitude, and longitude to x,y,z.
- Calculate distance using Euclidean distance formula
Comments