Tilted cylindrical tank volume
Calculates volume of cylindrical tank tilted at an angle. To perform calculation you must provide the tank size, angle and liquid level.
To perform the calculation, you must provide the tank size, angle, and liquid level.
Liquid level measurement
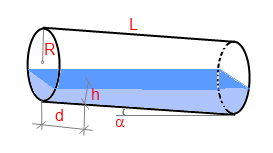
You must measure the liquid level at the middle line of the tank perpendicular to the tank's bottom. (see picture). You may measure the liquid level at any distance from one of the bases (If you do, you must enter the distance in a special parameter).
Alternatively, you may tilt the tank to make the zero liquid level at the top base; in this case, you must measure the tilt angle only.
You may find calculation details and formulas below the calculator.
I could not find a ready solution to calculate liquid volume in a tilted cylinder, so I derived the formula in this way:
Partially filled tilted tank volume formula
where - how the segment angle depends from the cylinder length x,
It can be derived as:
where
a - tilt angle,
h0 - liquid level at the upper base
If we substitute this expression in the formula we get:
where
If we take the integral we get the solution:
where
,
Determine tank part length filled with liquid
The above formulas are used for tilted tank volume calculation with these assumptions:
- Both bases partially filled with liquid.
- The liquid level h0 is measured directly on the upper base.
- No part of the tank is dry or fully filled.
But the calculator accepts the liquid level measured on some distance near the upper or lower base. Some parts of the tank can be dry or fully filled.
To calculate liquid level directly on the upper base hu use formulas:
where hll - liquid level measured on the distance ll from the lower base, Lc - length of the tank
where hlu - liquid level measured on the distance lu from the upper base.
If the hu is equal or above zero we assume h0=hu, and Lf = Lc.
Empty tank part
Otherwise, the hu can be negative. That means some tank part is empty. In this case assume h0=0 and calculate remained (filled) part Lf using formula:
where Lc is cylinder length.
Fully filled part
The liquid level directly on the lower base h1 can be determined as:
If calculated h1 value is greater than tank diameter, some part of our cylinder is fully filled with liquid. So we need to calculate fully filled part length as:
Fully filled part volume calculation is trivial see Cylinder
After these calculations you may substitute partially filled tank length and liquid level h0 in the first section formulas to calculate partially filled tilted tank part volume.
Comments