Capacitor in Direct Current Circuit
These online calculators computes various parameters for charging and discharging the capacitor with the resistor
This content is licensed under Creative Commons Attribution/Share-Alike License 3.0 (Unported). That means you may freely redistribute or modify this content under the same license conditions and must attribute the original author by placing a hyperlink from your site to this work https://planetcalc.com/1980/. Also, please do not modify any references to the original work (if any) contained in this content.
These online calculators computes various parameters for charging and discharging the capacitor with the resistor. Formulae used for calculations are below the calculators.
Below is the picture of electrical circuit for charging the capacitor with the power supply unit.
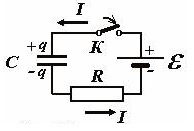
After switch K is closed, direct current starts charging the capacitor.
According to Ohms law, the sum of capacitor and resistor voltages is equal to power supply voltage.
The capacitor charge and current depend on time. At the initial moment, there is no charge at the capacitor, thus, current is maximum, as well as power dissipation on the resistor.
During charging, capacitor voltage changing according to the following equation
where tau
is called Time Constant. Since charging is infinite process, usually, a capacitor is considered to be fully charged after 5 time constants. After 5 time constants, the capacitor will be charged to 99.2% of the supply voltage.
Capacitor Charge
Capacitor Energy
Work of Power Supply
Comments