Calculation of the edge cut margin to obtain an octagonal face

A one-line calculator, the purpose of which cannot be explained without a picture. So, the problem is as follows: there is a square cross section bar. It should be so sawed off at the edges that the end face becomes an octahedron (a regular octagon). Sawing is done at a known angle of 45 degrees. Now look at the picture:

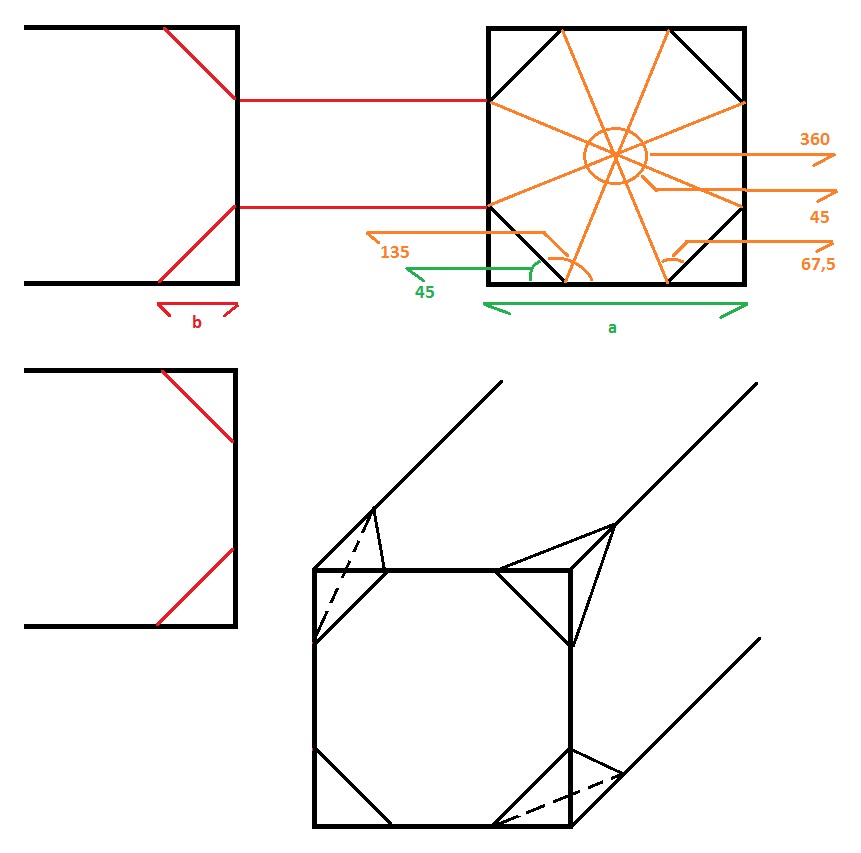
You can see that the angle marked in green is 45 degrees. The width of the whole side is known - this is the width of the bar. The cut also goes at 45 degrees. We saw off, thus, a correct pyramid, with the octagon at its base, and the angle between the edge and the side of the base is also equal to 45.

That is, our indentation from the edge is:

Where s is the side of the octagon.

The side of the octagon relates to the width of the bar as:

Thus, the final formula is:

Calculation of the edge cut margin to obtain an octagonal face

Bar size

Calculation precision

Digits after the decimal point: 1

Calculate

Cut edge indentation

 

 Link  Save  Widget