Newton's method
This online calculator implements Newton's method (also known as the Newton–Raphson method) for finding the roots (or zeroes) of a real-valued function.
It implements Newton's method using derivative calculator to obtain an analytical form of the derivative of a given function because this method requires it. You can find a theory to recall the method basics below the calculator.
Newton–Raphson method1
In numerical analysis, Newton's method (also known as the Newton–Raphson method), named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots (or zeroes) of a real-valued function.
The method starts with a function f defined over the real numbers x, the function's derivative f ′, and an initial guess x0 for a root of the function f. If the function satisfies the assumptions made in the derivation of the formula and the initial guess is close, then a better approximation x1 is
Geometrically, (x1, 0) is the intersection of the x-axis and the tangent of the graph of f at (x0, f(x0)).
The process is repeated as , until a sufficiently accurate value is reached.
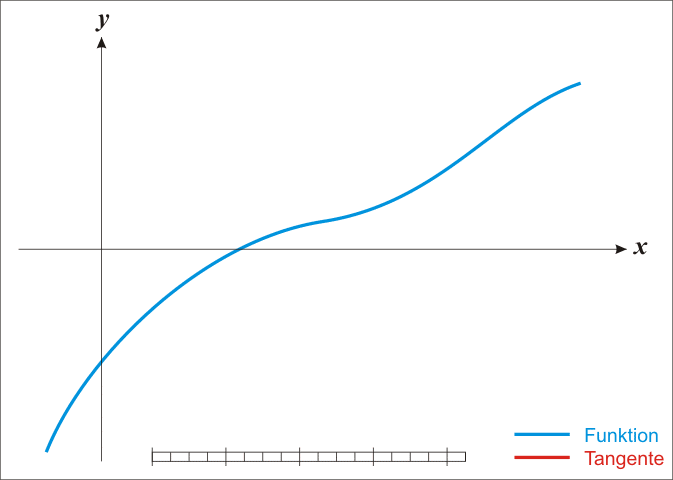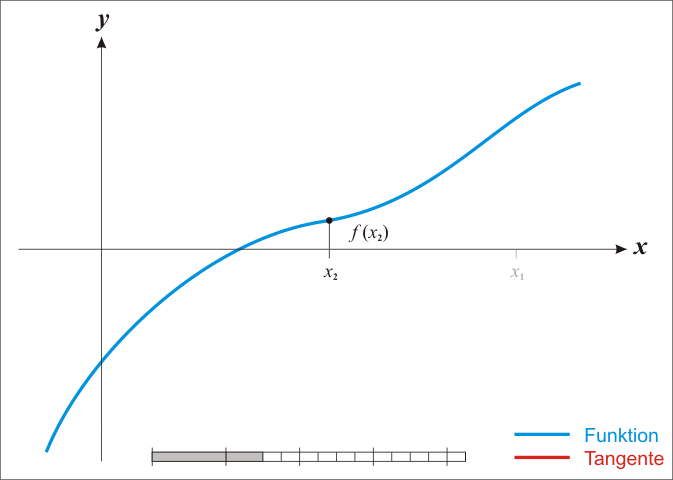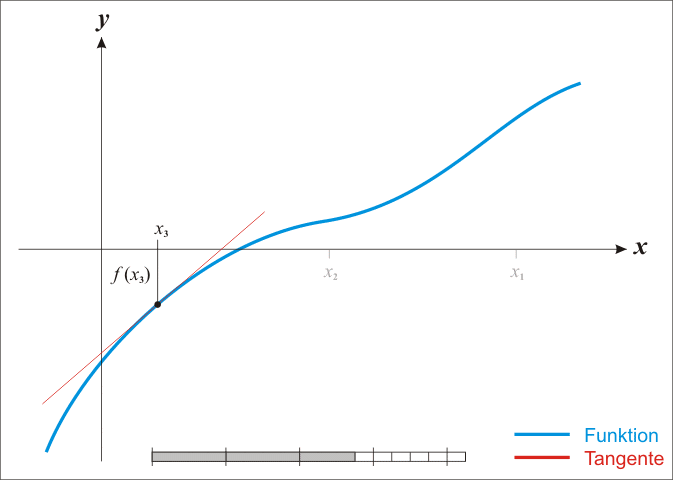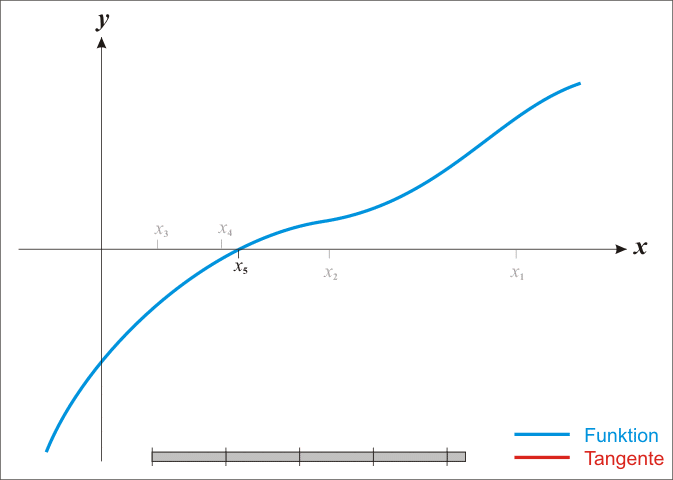
The idea of the method is as follows: one starts with an initial guess which is reasonably close to the true root, then the function is approximated by its tangent line (which can be computed using the tools of calculus), and one computes the x-intercept of this tangent line (which is easily done with elementary algebra). This x-intercept will typically be a better approximation to the function's root than the original guess, and the method can be iterated.
Newton's method is an extremely powerful technique—in general the convergence is quadratic: as the method converges on the root, the difference between the root and the approximation is squared (the number of accurate digits roughly doubles) at each step. However, there are some difficulties with the method: difficulty in calculating derivative of a function, failure of the method to converge to the root, if the assumptions made in the proof of quadratic convergence of Newton's method are not met, slow convergence for roots of multiplicity greater than 1
Comments