Z-score from P-value
This online calculator calculates z score from p value
This online calculator calculates the z score from the p-value. Of course, there are some known values, like everybody (well, not everybody, but anyway) knows that the z score for 0.05 significance level is roughly 1.64. However, the calculator below can calculate the z score for an arbitrary p-value. It is not that hard if you can calculate the inverse of CDF (cumulative distribution function) for standard normal distribution. And I can, thanks to excellent jStat library.
Now, let me give you a couple of illustrations of how it works for various hypotheses.
Left-tail event
For the left-tail event, the p-value is the probability of obtaining a result equal to or less than observed x. In this case, the p-value is the value of the cumulative distribution function of x, as shown in the picture below.
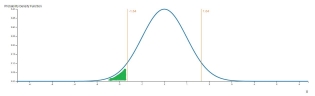
To find out the z-score, we need to get the inverse of CDF of the p-value.
Right-tail event
For the right-tail event, the p-value is the probability of obtaining a result equal to or greater than observed x. In this case, the p-value is the value of one minus the cumulative distribution function of x, as shown in the picture below.
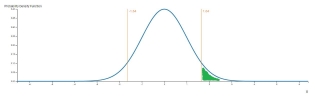
To find out the z-score, we need to get the inverse of CDF of one minus p-value.
Double-tail event
For the double-tail event, the p-value is the double probability of "smaller" of both. Knowing only the p-value, we assume that we are talking about symmetrical x values. In this case, the p-value can be found by doubling the CDF of left-tail x, as shown in the picture below.
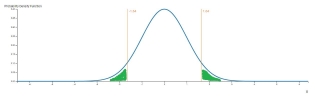
To find out the z-score, we need to get the inverse of CDF of the p-value divided by 2. Note that in this case, the calculator below displays modulo of Z-score.
Comments