Tips and tricks #9: Big numbers
How to use big number input and PCR library.
This content is licensed under Creative Commons Attribution/Share-Alike License 3.0 (Unported). That means you may freely redistribute or modify this content under the same license conditions and must attribute the original author by placing a hyperlink from your site to this work https://planetcalc.com/7826/. Also, please do not modify any references to the original work (if any) contained in this content.
Tips and tricks series
- Tips and tricks #1: How to set output value
- Tips and tricks #2: How to make calculator translatable into different languages
- Tips and tricks #3: How to make calculator with custom errors
- Tips and tricks #4: How to make calculator with table output
- Tips and tricks #5: How to show/hide input and output controls in a calculator
- Tips and tricks #6: How to make calculator with virtual keyboard
- Tips and tricks #7: How to make calculator with SVG image map
- Tips and tricks #8: How to reuse existing calculator
- Tips and tricks #9: Big numbers
- Tips and tricks #10: Files, long calculation mode
- Tips and tricks #11: Dynamic table columns
- Tips and tricks #12: Long (infinite) calculations
- Tips and tricks #13: Bitmaps and Pixel manipulation
- Tips and tricks #14: How to use a masked input
This article may rely on knowledge you should get from previous articles, so you may want to check them first.
Browser JavaScript implementation has a limit of integer number exact representation: 9007199254740991 or 253-1 or roughly 9 quadrillion. To overcome this limit big number libraries can be applied.
To work with big numbers PLANETCALC has a special input set: Big number and Big number array. The big number library underlying these inputs supports operations in an integer field, complex integer fields, and real, rational, or complex fractional ring. General Number output can be used to represent this library calculation results. The library is globally available in a calculator source code by PCR. prefix.
This library is internally based on big-integer library, which has a good performance, but PCR library was designed in idea to have a usable interface, the same overall supported fields rather than performance. So consider using the bigInt library directly, if your calculator requires the best performance. The Number output supports bigInt types as well.
The calculator below uses Big number input, Number output, and PCR library to calculate GCD using extended Euclidean algorithm:
PCR big number library overview by the Euclidean algorithm code example
The calculator has two big integer inputs, defined in the calculator editor as shown in the picture below:
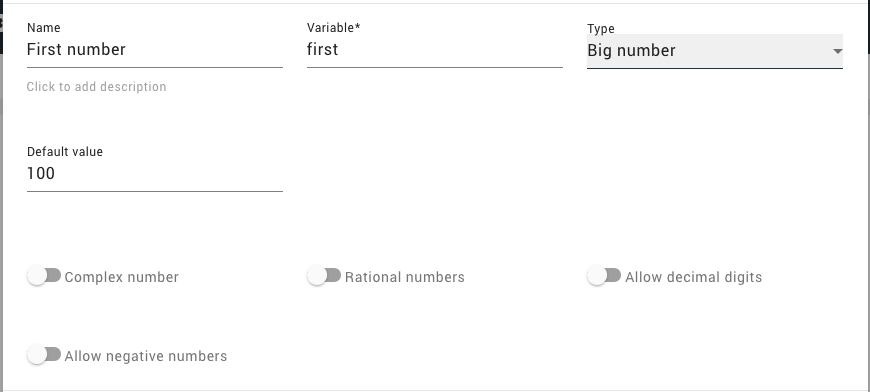
So first and second input variables are defined as PCR.integer by input editor. You may also define PCR numbers variables in code, see the calculator code fragment, which defines a placeholder for the result with three PCR integers:
var euklid = {
gcd: PCR.integer(1),
x: PCR.integer(0),
y: PCR.integer(0)
};PCR integers has a number of arithmetic operations. The code below demonstrates some of them (integer division: divmod, subtraction: sub and multiplication: mul).
function gcd (a, b, holder) {
if (a.eq(0) ) {
holder.x = PCR.integer(0);
holder.y = PCR.integer(1);
return b;
}
var q = b.divmod( a );
var d = gcd (q.r, a, holder);
var tx = holder.x;
holder.x = holder.y.sub(
q.q.mul( holder.x ) );
holder.y = tx;
return d;
}Besides arithmetics, PCR library has a number of compare operations defined over all PCR number types. The code fragment below demonstrates greater than (gt) operation:
euklid.gcd =gcd(first.gt( second ) ?
second : first, first.gt( second )
? first : second, euklid);To report the result to users just SetValue to a general Number output:
res.SetValue(euklid.gcd);
coef1.SetValue(euklid.y);
coef2.SetValue(euklid.x);The Number output can be configured to display either real or rational numbers. The rational numbers mode output having PCR big number value can be used for the precise number representation as a simple fraction. See the Result set switch on the following picture:

PCR big number library reference
Initialization
| Function | Example | Description |
|---|---|---|
| PCR.integer | var one = PCR.integer(1); | Big integer number definition |
| PCR.rational | var quarter = PCR.rational(1,4); | Rational number definition |
| PCR.complex | var complex = PCR.complex(7,3); //7+3i | Complex number definition |
| PCR.real | var real = PCR.real(3.1415926); | Real number definition |
| PCR.parse | var complexFraction = PCR.parse("1/3+i"); | Parses a string into PCR number. |
Operations
| Function | Example | Description |
|---|---|---|
| add | var two = PCR.integer(1).add(1); | Adds two PCR numbers. |
| sub | var twoThird = PCR.integer(1).sub(PCR.rational(1,3)); | Subtract two PCR numbers |
| neg | var minusOne = PCR.integer(1).neg(); | Negates a PCR number |
| mul | var complex = PCR.complex(7,3).mul(2); //14+6i | Multiply two PCR numbers |
| div | var quarter = PCR.rational(1,2).div(2); | Divide two PCR numbers |
| divmod | var twoAndOne = PCR.integer(5).div(2); // returns {q:2,r:1} | Integer division with modulo |
| mod | var one = PCR.integer(5).mod(2); | Integer division modulo |
| idiv | var two = PCR.integer(5).idiv(2); | Integer division |
| abs | var one = PCR.integer(-1).abs(); | Absolute value |
| gcd | var two = PCR.integer(6).gcd(8); | Greatest common divisor |
Conversions
| Function | Example | Description |
|---|---|---|
| toString | var fraction = PCR.rational(1/3).toString(); // returns "1/3" | Converts PCR number into string. |
| toFixed | var fraction = PCR.rational(1/3).toFixed(2); // returns "0.33" | Floating point string representation with fixed decimal digits. |
| toTeX | var fraction = PCR.rational(1/3).toTeX(); // returns "\frac{1}{3}" | LaTeX representation. |
Comparsions
| Function | Example | Description |
|---|---|---|
| isZero | var zero = PCR.rational(1/2).sub(0.5).isZero(); | Compare a PCR number with zero. |
| compare | var greater = PCR.rational(1/2).compare(0.3); | Compare two values, returns 1 if the left operand is greater, returns -1 - if the left operand is less, and 0 - if both operands are equal . |
| eq | var equal = PCR.rational(1/2).eq(0.5); | Equality. |
| gt | var greater = PCR.rational(1/2).gt(0.3); | Greater than. |
| gte | var greater = PCR.rational(1/2).gte(0.3); | Greater than or equal. |
| lt | var greater = PCR.rational(1/2).lt(0.3); | Less than. |
| lte | var greater = PCR.rational(1/2).lte(0.3); | Less than or equal. |
Comments