Synthetic division
Synthetic division is a simplified way of dividing a polynomial using only the coefficients of the terms in the polynomial. It is a shortcut method that avoids the need for long division or the use of the polynomial remainder theorem.
This content is licensed under Creative Commons Attribution/Share-Alike License 3.0 (Unported). That means you may freely redistribute or modify this content under the same license conditions and must attribute the original author by placing a hyperlink from your site to this work https://planetcalc.com/8091/. Also, please do not modify any references to the original work (if any) contained in this content.
This calculator performs synthetic division of any polynomials. You may find the method description just below the calculator.
Synthetic division preparation
The synthetic division preparation by example: 3x4+5x3+2x+4 / x2+2x+1.
| Preparation steps | |
|---|---|
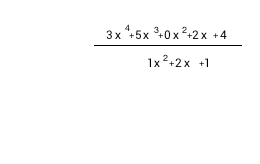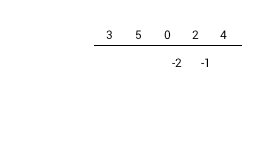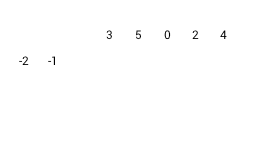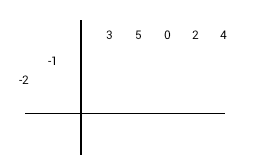 |
1) Negate divisor coefficients 2) Write dividend coefficients at the top (zero for missed terms). 3) Remove highest divisor coefficient. 4) Write remained divisor coefficients diagonally on the left |
Synthetic division method for monic divisors
The synthetic division with monic divisor by example: 3x4+5x3+2x+4 / x2+2x+1.
| Division algorithm for monic divisor | |
|---|---|
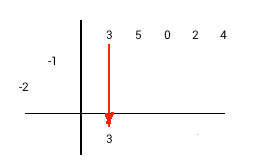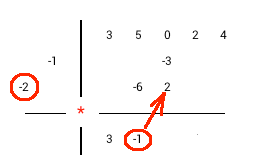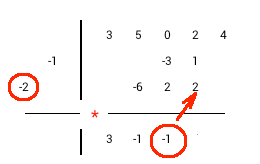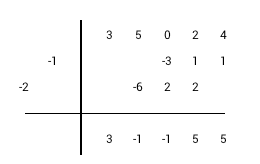 |
1) Drop highest dividend coefficient in the first column of result row 2) Multiply divisor diagonal by the last column value of result row 3) Place multiplication result diagonally to the right from the last result column 4) Perform addition in the next column and write the sum in the same column of result row 5) Repeat steps 2-4 until you would go past the columns at the top row. 6) Sum values in any remaining columns and write the result in result row. 7) Separate result and remainder. A number of terms in the remainder equal a number of divisor terms minus one. |
Non-monic divisors
The synthetic division with non-monic divisor example: 3x3+5x2+7x+2 / 3x2-x-2.
| Division algorithm for non-monic divisor | |
|---|---|
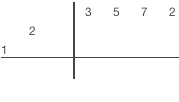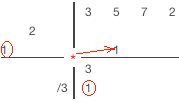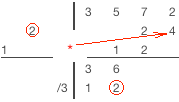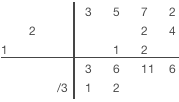 |
1) Drop highest dividend coefficient in the first column of remainder row 2) Divide last column value in a remainder row by the first divisor coefficient, write the result in result row 3) Multiply divisor diagonal by the last column value of result row 4) Place multiplication result diagonally to the right from the last result column 5) Perform addition in the next column and write the sum in the same column of remainder row 6) Repeat steps 2-5 until you would go past the columns at the top row. 7) Sum values in any remaining columns and write the result in a remainder row. 8) Separate result and remainder. Result coefficient will be in the last row. Remainder coefficients are in the previous row. A number of terms in the remainder equal to a number of divisor terms minus one. |
Comments