Liquid volume in a rectangular tank
The calculator gives the liquid volume in a partially filled rectangular tank, pitched and turned by the given angles.
Use this calculator to get the volume of liquid in a rectangular tank. The tank can be tilted along length and width edges.
The tilt angle can be set in three ways:
- in degrees of tilt angle
- by the elevation distance of the tank corner
- by the liquid depth, measured in 3 different points ( the points must not lay on the same straight line ).
Please note, the elevation and the liquid depth must be measured perpendicular to the tank's base, regardless of the angle of its inclination.
The calculation formulas are described just below the calculator.
Tank dimensions
Tilt
Liquid level at the deepest corner
Liquid level at a corner
Liquid level at the corner adjacent to the first one in length
Liquid level at the corner adjacent to the first one in width
Tilted rectangular tank model
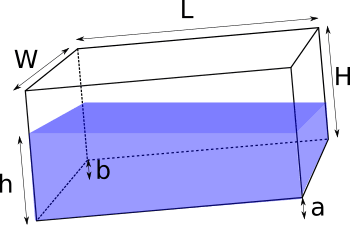
The tank dimensions
L - length
W - width
H - height
Tilt and liquid level
a - distance of the elevation of the corner adjoining the deepest in length
b - a distance of the elevation of the corner adjoining the deepest in width
h - liquid level in the deepest corner
Formulas of the liquid volume in the tilted rectangular tank
Assuming the deepest corner of the rectangle as the origin and the x-axis coincides with the edge L, y-axis coincides with the edge W, and z-axis coincides with the edge H, we can define the liquid surface plane equation as:
It is not difficult to derive the volume formula for a tank tilted and filled with liquid, as in the picture above.
If you increase the inclination angles and change the amount of liquid, the problem becomes more complicated.
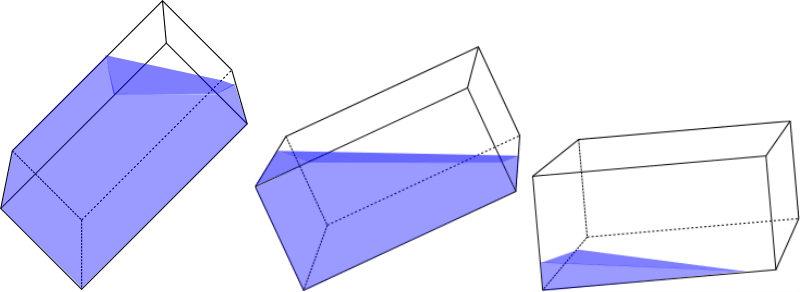
One edge inclination case(a>0, b=0)
The liquid volume equals area of liquid section multiplied by the tank width:
,
where
Two edges inclination case(a>0, b>0)
Instead of deriving the formulas for each possible liquid shape, you may notice that the liquid form in the tank is a truncated pyramid for any combination of liquid amount and inclination angles.
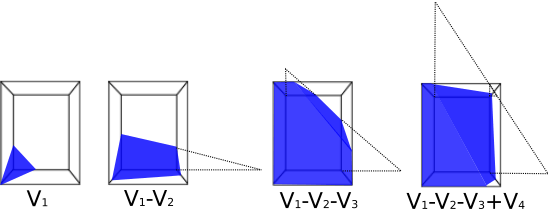
So the universal formula for the volume of liquid in an inclined rectangular tank is:
where:
Vi volumes of pyramids (or frustums) formed by three perpendicular planes coinciding with two walls and the base of the tank and one inclined plane coinciding with the surface of the water
V1 - volume of the pyramid (frustum) with the apex at the deepest tank corner x,y =(0,0)
V2 - volume of a pyramid (frustum) with apex at the corner bordering the deepest in length x,y =(L,0)
V3 - volume of a pyramid (frustum) with apex at the corner bordering the deepest in width x,y =(0,W)
V4 -volume of a pyramid with apex in the corner, diagonally opposite the deepest x,y = (L,W)
To find each volume we must calculate
- the water surface level at the apex:
- the length of bottom base (z=0)
- the the length of the top base z=H
- the width of bottom base (z=0)
- the width of the top base z=H
Then we calculate the volume by the frustum or pyramid volume formula:
where
Comments