Calculation of geometric characteristics of flat sections of simple shapes
This online calculator calculates static moments, moments of inertia and radii of inertia for flat cross sections of simple shapes
This online calculator is designed to calculate the basic geometric characteristics of the simplest flat cross-sections. The calculator displays the static moment, moment of inertia and radius of inertia in x and y axes, as well as the coordinates of the center of gravity and the cross-sectional area. The theory and calculation formulas can be found below the calculator.
Lower left corner
Top right corner
Center
Radius
Vertex at the right angle
Second vertex
Third vertex
The general calculation algorithm is as follows:
- Determination of the center of gravity of the cross section
- Determination of the cross-sectional area
- Determination of static moment
- Determination of axial moment of inertia
- Determination of the radius of inertia
Static moment of section 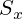 ,
, 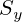 .
.
The physical meaning of static moment: if each simple figure of which a complex figure is composed is endowed with a weight, they will represent a system of parallel forces and each of them will create its moment relative to some axis with a shoulder equal to the distance from the axis to the center of gravity of this simple figure. If the force is replaced by the area, the moment turns from force to a geometric index called static moment.1 Measured in units of length in cube (cm³), it can be positive, negative, and zero.
In general, the mathematical notation of static moments with respect to the x- and y-axis is as follows:
For special cases where the figure in question is a simple geometric figure, the integral notation can be replaced by a simpler one, then the formulas look like this:
Where A is the cross-sectional area.
,
are the distance from the x and y axes to the centre of gravity of the simple figure.
The center of gravity of a rectangle is located at the point where its diagonals intersect. The center of gravity of a circle coincides directly with the center of the circle itself, and finding the center of gravity for a triangle can be found in this calculator.
Axial moment of inertia
The axial moment of inertia of the area of a section is the integral of the products of the elementary areas of a given section by the squares of their distances from the axis under consideration. The value of the axial moment of inertia is always positive. The formulas for the axial moment of inertia are:
The moment of inertia of a figure about an axis passing through its center of gravity is called the central, or proper, moment of inertia. If a figure consists of several simple figures, the axes drawn through the center of gravity of the whole figure are called the principal central axes. The moments of inertia about the principal central axes are called principal central moments.
Here are the formulas for the principal central moments of each of the simplest sections used in the calculator
Rectangle
- The cross-sectional area for a rectangle is found by the formula:
,
where b and h are the sides of the rectangle. - The moments of inertia
and
for the rectangle are found by the formulas:
To illustrate the derivation of the central moment formulas, consider the derivation of the above formula for the principal central moment of inertia for a rectangle.
The rectangular section has two axes of symmetry, and the principal central axes Cx and Cy pass through the midpoints of the parallel sides.
The principal central moment of inertia about the axis is as follows
whence
Similarly, we obtain:
.
Rectangular triangle whose cathetes are parallel to the axes
- The cross-sectional area for a right-angled triangle is found by the formula:
,
where b and h are the cathetes of the triangle.
3- The moments of inertiaand
for the triangle are found by the formulas:
Circle
- The cross-sectional area for a circle is found by the formula:
,
where r is the radius of the circle.
3- The moments of inertiaand
for a circle are found by the formulas:
To find the axial moment of inertia with respect to an arbitrary axis, we use the Huygens-Steiner theorem: the moment of inertia of a body with respect to an arbitrary axis is equal to the sum of the moment of inertia with respect to an axis parallel to this axis and passing through the center of gravity (central moment) and the product of the area of the body by the square of the distance between the axes. It is measured in units of length to the fourth degree (cm⁴).
Formulas:
Radius of inertia
Radius of inertia i is the distance from the corresponding axis to the point at which the concentration of the entire cross-sectional area will give the same moment of inertia as for the entire area of the figure in question. It is measured in units of length (cm).
Formulas:
Where A is the cross-sectional area,
,
- axial moments of inertia.
-
Technical mechanics for construction specialties: textbook for students of secondary vocational education / V.I. Setkov - M.: Publishing Centre "Academy", 2007. ↩
Comments