Simple beam support reaction
The calculator gives support reactions of the simple beam under various vertical load.
This online calculator finds support reactions of the simple beam under transverse loads. A simple beam is a rectangular beam, fixed on two supports: one - pinned ('A' support), the other - roller ('B' support). The calculator displays support reactions VA and VB, moment equilibrium equations, and draws the beam system. Note: The distance to 'A' support value must be negative for the force acting to the left of the 'A' support. The theory and calculation formulas are below the calculator.
Load
| Distance to the support A | Load | Value | Direction | Moment direction | Range | Difference | ||
|---|---|---|---|---|---|---|---|---|
Support reactions
Under the influence of loads, opposing forces occur in the beam supports, called support reactions. These forces depend on the type of load and the type of supports.
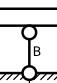
The roller support (in our model designated as "B") allows the beam to move freely in the horizontal plane and prevents vertical movement. Therefore, it has only a vertical reaction VB.
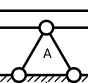
A pinned support is attached to the beam. It prevents its horizontal and vertical movement. In the presence of forces acting on the beam in the horizontal plane, this support additionally produces a horizontal reaction. Our model allows only transverse forces acting on the beam, so the horizontal reaction of the 'A' support will always be zero. We denote the vertical reaction of the support A by VA .
Equilibrium Equations
As we know from statics, all forces and moments of forces in a fixed system are balanced. Therefore, the sums of forces and moments at any point of this system are equal to zero.
All forces under a transverse load on a simple beam act parallel to the Y-axis. Therefore, one can draw only two independent equilibrium equations for the projection of forces on the Y-axis. It is quite enough to find two unknown support reactions: VA and VB.
When writing equilibrium equations, we have a choice:
- compose one equation of equilibrium of the projection of forces and one equation of the moments balance at some point
- compose two equations of equilibrium of moments at two points.
Let's use the second method, and leave the first one to check the result.
It is most convenient to draw up equations for points of supports A and B:
Recall that the moment of force at a certain point is the product of the force F by the shortest distance from this point to the line of action of the force (lever) l:
Based on this, the equilibrium equations for the moments at points A and B for the system of transferse forces F1 ... Fn acting on the beam take the form:
Where Fi is the magnitude of the force or support reaction in Newtons. liA and liB - the lever in meters (the shortest distance from the point of application of force i to the support A or B respectively). siA and siB are the sign of the moment of force i at points A or B, respectively.
The rule for choosing the signs of the moments: the sign is positive (+1) for the moment bending the beam around the selected point clockwise ↻ and negative (-1) for the opposite direction ↺. You can also choose opposite values, then the equations will take a slightly different form, but the final result will not change.
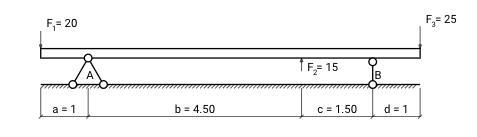
For example, for the system of forces shown by the figure above, the equilibrium equations can be written as follows:
Calculating, we get the values of the support reactions: V A = 15.42 and V B = 14.58. Let's check that the sum of all forces is equal to zero (for forces acting downwards - the sign is positive, for those acting upwards - negative):
When composing the equations, we assume the reactions of both supports are directed upward. Calculating, it may turn out that the reaction of a support turns out to be negative. This means that the reaction of such a support must point opposite direction. (The sum of the moments of forces acting on the beam tries to tear it away from the support.)
Distributed load
Sometimes it is required to specify a load distributed in a certain way over a segment of length a. For the purpose of calculating the support reactions, such a load can be replaced by its resultant force. The point of application of such a force is located at the center of mass of the distributed load shape. The modulus is calculated by integrating the load distribution function in a given range. For simple functions, the module can be easily expressed in terms of a given load rate.
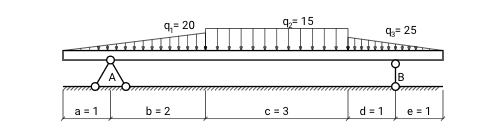
The table below shows the formulas for the modulus of the concentrated resultant force and the points of its application for all types of distributed loads supported by the calculator:
| Load | Module | Application point |
|---|---|---|
| Uniform | 1/2 a | |
| Linearly decreasing | 1/3 a | |
| Linearly increasing | 2/3 a |
In the formulas above, q is the load intensity in N / m, a is the range of the distributed load. Note: the point of application of the force is measured from the beginning of the range of the distributed load. The intensity of a linearly distributed load is set for the section of maximum load (we assume that at the point of minimum, intensity = 0).
After calculating the modulus and lever of the resultant distributed load, they can be substituted into the equations of moments, just as we did with concentrated forces.
Concentrated moment
Another way to set the load in the calculator is by using a moment in Nm applied to a point. The value of the concentrated moment is added to the equilibrium equations with a sign determined by the direction of the moment according to the rule of signs. The point of application of the concentrated moment is irrelevant for calculating the support reactions.
Comments