Calculation of fluid flow rate as it flows out of the orifice at constant head.
This online calculator calculates the flow rate of a liquid as it flows through a small opening in a thin wall at a constant liquid level (head) in the tank.
Note that according to the textbook of Kudinov and Kartashov1 ($8.1), a wall is considered thin , if its thickness is less than 0.2d, where d is the diameter of the hole. The opening is considered small if the area of the opening does not exceed 0.1ω1, where ω1 is the area of the cross section of the vessel. Also included in the formula is the flow coefficient - for small circular holes in the thin wall, the flow coefficient is on average 0.60 - 0.62. Read more about the calculation formula and the different consumption factor values below the calculator.
Flow through a small hole in a thin wall
In the case of fluid flow through a hole, we are primarily interested in the flow rate of the flowing fluid. The flow rate, in turn, is determined by the velocity of the fluid - as the product of the actual velocity of the fluid by the cross-sectional area of the hole. In the case of an ideal fluid (a fluid in which there is no viscosity or heat conduction), the flow rate is determined by Torricelli's formula
where g is the acceleration of free fall, h is the head height, or the height of the liquid level above the centre of gravity of the unflooded orifice.
And the flow rate of the ideal fluid Q is
where ω is the cross-sectional area of the orifice.
For a real fluid, a velocity coefficient ϕ is introduced into the Torricelli formula, depending on the coefficient of hydraulic resistance at the entrance to the orifice
And in the formula for the fluid flow rate - the jet compression coefficient α, i.e. the ratio of the compressed cross-sectional area of the jet to the area of the orifice, see the figure below.
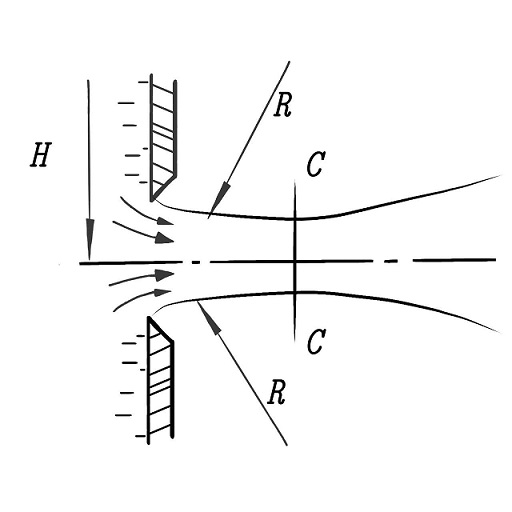
The compression of the jet is due to the inertia of the fluid particles moving along curvilinear trajectories2 when approaching the orifice ($4.9).
The product of α and ϕ is called the flow coefficient μ
For viscous fluids and low flow velocities, the coefficients α, ϕ and hence μ will depend on the Reynolds number.
The Reynolds number characterises the ratio of inertial forces to viscous friction forces in viscous liquids and gases, and is calculated through the density of the medium, the characteristic velocity, the hydraulic diameter and the dynamic viscosity of the medium. For each type of flow there is some critical value of Reynolds number, up to which the flow is characterised by laminar flow, i.e. liquid or gas moves in layers without mixing and pulsations, when crossing which the flow becomes unstably turbulent, and with further increase of Reynolds number of the flow - steadily turbulent.
At large Reynolds numbers (>104, turbulent regime) the flow coefficients are constant, depend only on the type of orifice, are determined experimentally and are given in reference books.
For example, Zinoviev's reference book3 (6. Hydromechanics, Table 24) gives the following values of the flow coefficient μ:
| Type of orifices and nature of fluid flow | μ |
|---|---|
| Small orifices with full compression | 0.6 |
| Medium sized holes with jet compression on all sides (in the absence of guide walls) on average | 0.65 |
| Holes in a vertical wall directly at the bottom with significant influence of lateral compression but no compression at all along the bottom | 0.65 - 0.70 |
| Same but with moderate lateral compression | 0.70 - 0.75 |
| The same with smooth lateral approaches | 0.80 - 0.85 |
The flow coefficient can be influenced by nozzles. A nozzle is a short pipe, 3 to 5 orifice diameters long, connected to the orifice. A cylindrical nozzle, for example, creates a swirl zone at the inlet and reduces the velocity coefficient. A conical converging nozzle achieves a flow coefficient of 0.95, a conical diverging nozzle 0.47 (depending on the angle) and a conoidal nozzle 0.98! For calculations, of course, the cross-section at the nozzle outlet is taken.
-
Kudinov V.A., Kartashov E.M. Hydraulics. Textbook for universities. Moscow: Vysshaya Shkola, 2004. 180 p.: ill. ↩
-
Course of lectures on the discipline "Hydraulics" for full-time students of construction specialities (technology 30/70) / Compiled by A.V. Kalinin, I.A. Lushkin - Togliatti: TSU, 2007. ↩
-
Concise technical reference book under the general editorship of Vyach A. Zinoviev. Part one. Moscow Leningrad: State Publishing House of Technical and Theoretical Literature, 1949. ↩
Comments