Regular Polygon Incircle and Circumcircle Calculator
This page presents two online calculators: the Incircle of a regular polygon calculator and the circumcircle of a regular polygon calculator.
Theory and formulas can be found below the calculators.
The incircle of a regular polygon calculator is a tool that helps in finding the properties of the incircle for any regular polygon, given the side length and the number of sides. This calculator provides the incircle radius, incircle area, polygon area, and incircle to polygon area ratio.
The circumcircle of a regular polygon calculator is a tool that calculates the parameters of the circumcircle of a regular polygon. Given the side length and the number of sides of the polygon, this calculator can determine the radius of the circumcircle, the area of the circumcircle, the area of the polygon, and the ratio of the circumcircle area to the polygon area.
The incircle and the circumcircle of a regular polygon
The incircle of a regular polygon is a circle that is tangent to all sides of the polygon.
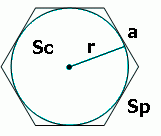
The incircle radius is the distance from the center of the incircle to any side of the regular polygon.
The area of the regular polygon can be calculated from the radius of the incircle like this:
The circumcircle of a regular polygon is the circle that passes through all the vertices of the polygon.
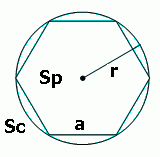
The radius of the circumcircle is the distance from the center to any vertex of the polygon.
The area of the regular polygon can be calculated using the formula (you do not need the radius of the circumcircle for that)
Comments