False position method
The false position method is a root-finding algorithm that uses a succession of roots of secant lines combined with the bisection method to approximate a root of a function f.
This content is licensed under Creative Commons Attribution/Share-Alike License 3.0 (Unported). That means you may freely redistribute or modify this content under the same license conditions and must attribute the original author by placing a hyperlink from your site to this work https://planetcalc.com/3712/. Also, please do not modify any references to the original work (if any) contained in this content.
A brief false position method description can be found below the calculator
False position method
False position method or 'regula falsi' method is a root-finding algorithm that combines features from the bisection method and the Secant method.
As in the secant method, we use the root of a secant line (the value of x such that y=0) to compute the next root approximation for function f.
The derivation of recurrence relation is the same as in the secant method:
Suppose we have starting values x0 and x1, with function values f(x0) and f(x1).
The secant line has the equation
Hence the root of the secant line (where у=0) is
The above formula is also used in the secant method, but the secant method always retains the last two computed points, while the false position method retains two points that always bracket a root.
A graphical interpretation can be seen below.
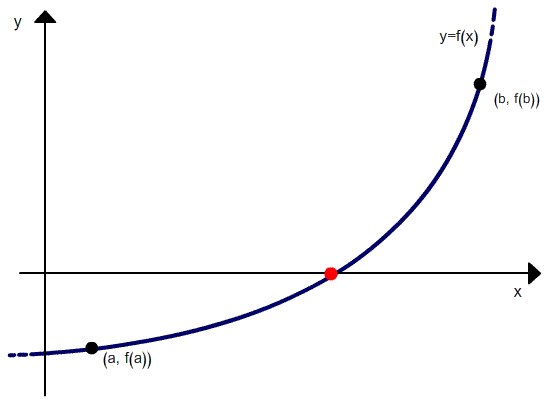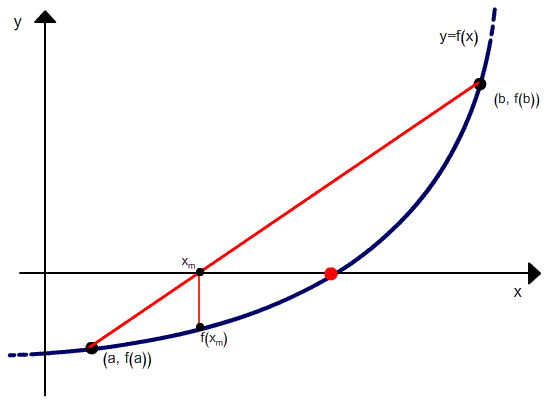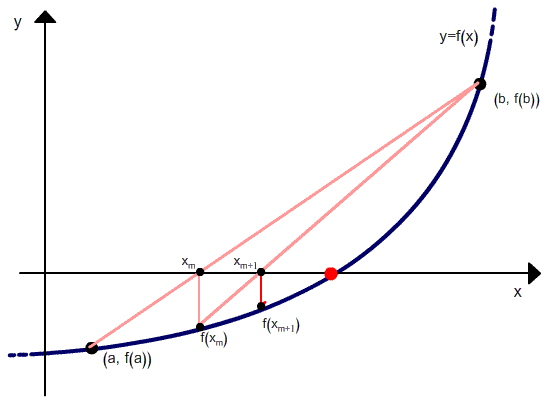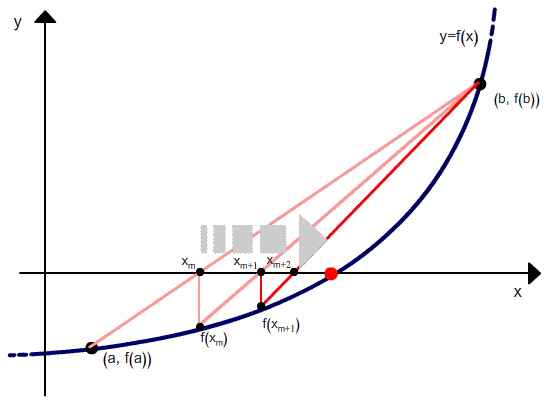
As can be seen from the recurrence relation, the false position method requires two initial values, x0 and x1, which should bracket the root. But unlike the bisection method, the width of the bracket does not tend to zero with iterations.
The tolerance condition can be either:
— function value is less than ε.
— difference between two subsequent хk is less than ε. Note that this is the difference between two calculated subsequent xk, not the end-points of the interval.
More: False position method
Comments