Cone development
Calculator of right circular cone / truncated right circular cone development
This page exists due to the efforts of the following people:
 | Timur
|
 | Michele
|
Anton
|
This content is licensed under Creative Commons Attribution/Share-Alike License 3.0 (Unported). That means you may freely redistribute or modify this content under the same license conditions and must attribute the original author by placing a hyperlink from your site to this work https://planetcalc.com/3831/. Also, please do not modify any references to the original work (if any) contained in this content.
The calculator computes parameters of a right circular cone or truncated right circular cone development. The picture below illustrates the task.
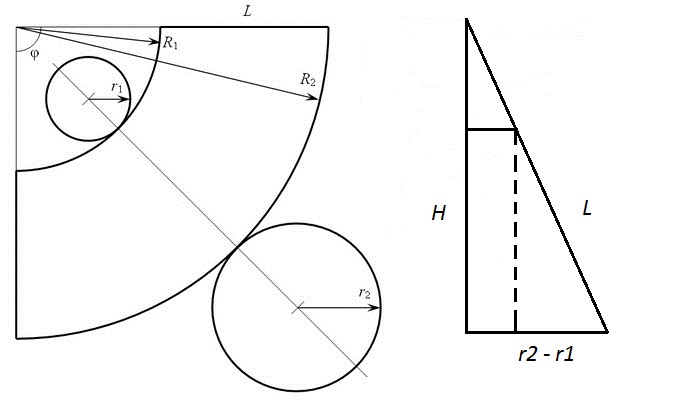
We have the lower base radius, radius of the upper base (in case of a truncated cone), and cone height. We need to find the length of the lateral side (or slant height), the lower arc radius, the radius of the upper arc (again, in case of a truncated cone), and the common central angle.
Slant height can be found using Pythagoras.
,
for the full cone r1 is zero.
Radius of the upper arc can be found using triangles similarity.
,
and for the full cone it is zero.
The radius of the lower arc thus
,
and for the full cone, it equals L
And central angle
Comments