Two arguments arctangent
The calculator gives an angle between positive axis x and the ray to the given point from point 0. The result corresponds to atan2 function, implemented in many computer languages and math libraries.
This page exists due to the efforts of the following people:
Anton
| |
 | Timur
|
This content is licensed under Creative Commons Attribution/Share-Alike License 3.0 (Unported). That means you may freely redistribute or modify this content under the same license conditions and must attribute the original author by placing a hyperlink from your site to this work https://planetcalc.com/7955/. Also, please do not modify any references to the original work (if any) contained in this content.
Some math problems, e.g., complex number argument, require calculating the angle between the ray to the given point and positive semi-axis x. Many computer languages, e.g., javascript, have an atan2 (two-arguments arctangent) function to solve this task. Atan2 returns the angle in the range (-π, π] in contrast to ordinal arc tangent, which result is in -π/2 .. π/2.
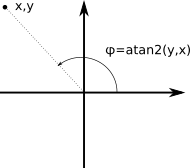
atan2 is based on the arctangent function, but it expects two arguments to correctly determine the resulting quadrant.
atan2
Atan2 calculation algorithm
Arctan2 with all positive x is same as ordinal arc tangent:
, x>0
For other x values, arctan2 can be calculated according the following table:
| y<0 | y = 0 | y>0 | |
|---|---|---|---|
| x<0 | |||
| x=0 | undefined |
Comments