Find the intersection of two circles
This online calculator finds the intersection points of two circles given the center point and radius of each circle. It also plots them on the graph.
To use the calculator, enter the x and y coordinates of a center and radius of each circle.
A bit of theory can be found below the calculator.
Circles intersection
The task is relatively easy, but we should take into account the edge cases – therefore we should start by calculating the cartesian distance d between two center points, and checking for edge cases by comparing d with radiuses r1 and r2.
Here are the possible cases (distance between centers is shown in red):
| Case | Description | Rule |
|---|---|---|
| Trivial case: the circles are coincident (or it is the same circle) | ||
 |
The circles are separate | |
 |
One circle is contained within the other | |

 |
Two intersection points | You have one or two intersection points if all rules for the edge cases above are not applied |

 |
One intersection point | Trivial case of two intersection points |
So, if it is not an edge case, to find the two intersection points, the calculator uses the following formulas (mostly deduced with Pythagorean theorem), illustrated with the graph below:
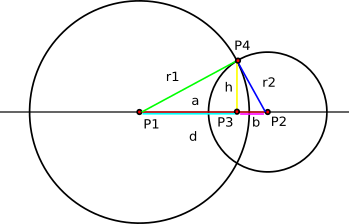
The first calculator finds the segment a
and then the segment h
To find point P3, the calculator uses the following formula (in vector form):
And finally, to get a pair of points in case of two points intersecting, the calculator uses these equations:
First point:
Second point:
Note the opposite signs before the second addend
For more information, you can refer to Circle-Circle Intersection and Circles and spheres
Comments