PLANETCALC Online calculators

Login
StudyMathGeometry

Ellipsoid

Calculates ellipsoid and spheroid volume and surface area.

This page exists due to the efforts of the following people:

A

Anton

Timur

Timur

Created: 2009-08-30 17:04:19, Last updated: 2021-02-14 09:02:09
Creative Commons Attribution/Share-Alike License 3.0 (Unported)

This content is licensed under Creative Commons Attribution/Share-Alike License 3.0 (Unported). That means you may freely redistribute or modify this content under the same license conditions and must attribute the original author by placing a hyperlink from your site to this work https://planetcalc.com/149/. Also, please do not modify any references to the original work (if any) contained in this content.

Scalene ellipsoid

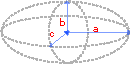
Ellipsoid dimensions
Ellipsoid dimensions

Ellipsoid is a sphere-like surface for which all cross-sections are ellipses.

Ellipsoids
Ellipsoids



Equation of standard ellipsoid body in xyz coordinate system is
{x^2 \over a^2}+{y^2 \over b^2}+{z^2 \over c^2}=1,
where a - radius along x axis, b - radius along y axis, c - radius along z axis.
The following formula gives the volume of an ellipsoid: {4 \over 3}\pi a b c
The surface area of a general ellipsoid cannot be expressed exactly by an elementary function. Knud Thomsen from Denmark proposed the following approximate formula: S\approx 4 \pi [(a^p b^p + a^p c^p + b^p c^p )/3]^{1\over p}, where p=1.6075

PLANETCALC, Ellipsoid

Ellipsoid

a semi-axis (radius) length
b semi-axis (radius) length
c semi-axis (radius) length
Digits after the decimal point: 5
Volume
 
Surface area (approx.)
 

Spheroids

If any two of the three axes of an ellipsoid are equal, the figure becomes a spheroid (ellipsoid of revolution). There are two kinds of spheroid: oblate spheroid (lens like) and prolate spheroid (сigar like).
Volume of spheroid is calculated by the following formula: {4 \over 3}\pi a^2 c

Unlike ellipsoids, exact surface area formulas exist for spheroids:

Oblate ellipsoid (spheroid)
Oblate ellipsoid (spheroid)



For oblate spheroid (a = b > c):
S=2\pi\left[a^2+\frac{c^2}{\sin(o\!\varepsilon)} \ln\left(\frac{1+ \sin(o\!\varepsilon)}{\cos(o\!\varepsilon)}\right)\right]
where angular eccentricity o\!\varepsilon=arccos ( {c \over a} )

Prolate ellipsoid (spheroid)
Prolate ellipsoid (spheroid)



For prolate spheroid (a = b < c):
S=2\pi\left(a^2+\frac{a c o\!\varepsilon}{\sin(o\!\varepsilon)}\right)
where angular eccentricity o\!\varepsilon=arccos ({a \over c} )

PLANETCALC, Spheroid

Spheroid

Digits after the decimal point: 5
Volume
 
Surface area
 
Angular eccentricity (grad)
 

The Earth's shape is similar to an oblate spheroid with a ≈ 6,378.137 km and c ≈ 6,356.752 km. According to the formula, Earth's surface is about 510050983.92 square kilometers.

URL copied to clipboard

Similar calculators

 Earth shape ellipsoid Engineering calculators Geometry spheroid surface area volume
PLANETCALC, Ellipsoid
Anton2021-02-14 09:02:09

Comments