Area of a quadrilateral
This article lists several calculators to compute the area of a quadrilateral
There are several ways to calculate the area of a quadrilateral
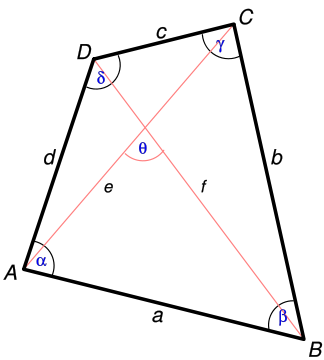
Picture: wikipedia
- Area of a quadrilateral given diagonals and angle between them. In this case, the formula will be
Calculator:
- Area of a quadrilateral given four sides and two opposite angles. In this case, it will be Bretschneider's formula
,
where s - semiperimeter
Calculator:
- Area of a quadrilateral given four sides and two diagonals. In this case, it will be non-trigonometric Bretschneider's formula
,
where s - semiperimeter
Calculator:
- Area of a quadrilateral given four sides and the fact that it is a cyclic quadrilateral. This is a particular case of Bretschneider's formula (we know that sum of two opposite angles are 180), known as Brahmagupta's formula
,
where s - semiperimeter
For this, you can use the calculator above by entering arbitrary angles whose sum is 180.
Proof for Bretschneider's formulas can be found here
And it is worth mentioning that it is impossible to find a quadrilateral area given ONLY four sides. You will need some additional conditions, like those above. Thus, based on many requests, we've created a model calculator that calculates quadrilateral areas by four sides - for an endless number of quadrilaterals. You can find it at Area of an irregular quadrangle with the given sides.
Comments