PLANETCALC Online calculators

Login
StudyMathGeometry

3d coordinate systems

Transforms 3d coordinate from / to Cartesian, Cylindrical and Spherical coordinate systems.

This page exists due to the efforts of the following people:

A

Anton

Timur

Timur

Created: 2018-10-22 12:49:06, Last updated: 2021-02-13 11:39:00
Creative Commons Attribution/Share-Alike License 3.0 (Unported)

This content is licensed under Creative Commons Attribution/Share-Alike License 3.0 (Unported). That means you may freely redistribute or modify this content under the same license conditions and must attribute the original author by placing a hyperlink from your site to this work https://planetcalc.com/7952/. Also, please do not modify any references to the original work (if any) contained in this content.

This calculator is intended for coordinates transformation from/to the following 3d coordinate systems:

  • Cartesian
  • Cylindrical
  • Spherical
    Cartesian, cylindrical, and spherical coordinate systems
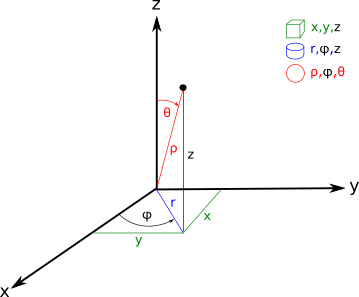
    Cartesian, cylindrical, and spherical coordinate systems

Cartesian coordinate system

A point can be defined in the Cartesian coordinate system with 3 real numbers: x, y, z. Each number corresponds to the signed minimal distance along with one of the axis (x, y, or z) between the point and plane, formed by the remaining two axes. The coordinate is negative if the point is behind the coordinate system origin.

Cylindrical coordinate system

This coordinate system defines a point in 3d space with radius r, azimuth angle φ, and height z. Height z directly corresponds to the z coordinate in the Cartesian coordinate system. Radius r - is a positive number, the shortest distance between point and z-axis. Azimuth angle φ is an angle value in range 0..360. It is an angle between positive semi-axis x and radius from the origin to the perpendicular from the point to the XY plane.

Spherical coordinate system

This system defines a point in 3d space with 3 real values - radius ρ, azimuth angle φ, and polar angle θ. Azimuth angle φ is the same as the azimuth angle in the cylindrical coordinate system. Radius ρ - is a distance between coordinate system origin and the point. Positive semi-axis z and radius from the origin to the point forms the polar angle θ.

PLANETCALC, Three-dimensional space cartesian coordinate system

Three-dimensional space cartesian coordinate system

Digits after the decimal point: 2

Cylindrical coordinates

Radius (r)
 
Azimuth (φ), degrees
 
Height (z)
 

Spherical coordinates

Radius (ρ)
 
Azimuth (φ), degrees
 
Polar angle (θ), degrees
 

Cartesian coordinates transformation formulas:

Radius in cylindrical system:
r = \sqrt{x^2+y^2}
Radius in spherical system:
\rho = \sqrt{x^2+y^2+z^2}
Azimuth angle:
\varphi=Arctan(y,x), see Two arguments arctangent

Polar angle:
\theta=\arctan\frac{\sqrt{x^2+y^2}}{z}

PLANETCALC, Cylindrical coordinates

Cylindrical coordinates

Digits after the decimal point: 2

Cartesian coordinates

x
 
y
 
z
 

Spherical coordinates

Radius (ρ)
 
Azimuth (φ), degrees
 
Polar angle (θ), degrees
 

Cylindrical coordinates conversion formulas:

To cartesian coordinates:
x=r\cos\varphi,
y=r\sin\varphi

Radius in spherical coordinate system:
\rho = \sqrt{r^2+z^2}
Polar angle:
\theta=Arctan(z,r), see Two arguments arctangent

PLANETCALC, Spherical coordinates

Spherical coordinates

Digits after the decimal point: 2

Cartesian coordinates

x
 
y
 
z
 

Cylindrical coordinates

Radius (r)
 
Azimuth (φ), degrees
 
Height (z)
 

Spherical coordinates transformation formulas

Cartesian coordinates:
x=\rho\sin\theta\cos\varphi,
y=\rho\sin\theta\sin\varphi,
z=\rho\cos\theta

Radius in cylindrical system:
r = \rho\sin\theta

URL copied to clipboard

Similar calculators

 #coordinates #geometry 3d Cartesian coordinates converters coordinate system coordinates cylindrical coordinates Geometry Math spherical coordinates
PLANETCALC, 3d coordinate systems
Anton2021-02-13 11:39:00

Comments