3d coordinate systems
Transforms 3d coordinate from / to Cartesian, Cylindrical and Spherical coordinate systems.
This calculator is intended for coordinates transformation from/to the following 3d coordinate systems:
- Cartesian
- Cylindrical
- Spherical
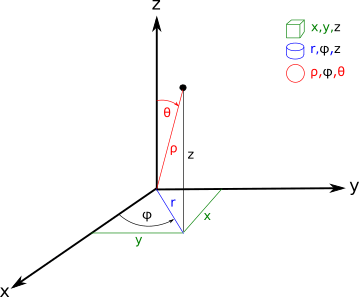
Cartesian, cylindrical, and spherical coordinate systems
Cartesian coordinate system
A point can be defined in the Cartesian coordinate system with 3 real numbers: x, y, z. Each number corresponds to the signed minimal distance along with one of the axis (x, y, or z) between the point and plane, formed by the remaining two axes. The coordinate is negative if the point is behind the coordinate system origin.
Cylindrical coordinate system
This coordinate system defines a point in 3d space with radius r, azimuth angle φ, and height z. Height z directly corresponds to the z coordinate in the Cartesian coordinate system. Radius r - is a positive number, the shortest distance between point and z-axis. Azimuth angle φ is an angle value in range 0..360. It is an angle between positive semi-axis x and radius from the origin to the perpendicular from the point to the XY plane.
Spherical coordinate system
This system defines a point in 3d space with 3 real values - radius ρ, azimuth angle φ, and polar angle θ. Azimuth angle φ is the same as the azimuth angle in the cylindrical coordinate system. Radius ρ - is a distance between coordinate system origin and the point. Positive semi-axis z and radius from the origin to the point forms the polar angle θ.
Cartesian coordinates transformation formulas:
Radius in cylindrical system:
Radius in spherical system:
Azimuth angle:
, see Two arguments arctangent
Polar angle:
Cylindrical coordinates conversion formulas:
To cartesian coordinates:
,
Radius in spherical coordinate system:
Polar angle:
, see Two arguments arctangent
Spherical coordinates transformation formulas
Cartesian coordinates:
,
,
Radius in cylindrical system:
Comments