Is a point in a triangle?
The calculator determines if an arbitrary point lies inside 2D triangle. The triangle is defined by 3 cartesian coordinate pairs.
This page exists due to the efforts of the following people:
Anton
| |
 | Timur
|
This content is licensed under Creative Commons Attribution/Share-Alike License 3.0 (Unported). That means you may freely redistribute or modify this content under the same license conditions and must attribute the original author by placing a hyperlink from your site to this work https://planetcalc.com/8108/. Also, please do not modify any references to the original work (if any) contained in this content.
The calculator below determines if a given point is inside a 2D triangle. The calculator uses a simple algorithm based on vector cross-product features. The algorithm detailed description is right behind the calculator.
Point in triangle
Cross products (z-coordinate)
A point inside a triangle. The algorithm description
3-dimensional vectors a and b cross product result for the right orthonormal basis is defined as:
[1].
Cross product is anticommutative:
It is an important feature to solve the point and triangle problem.
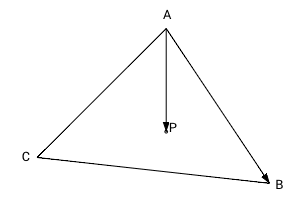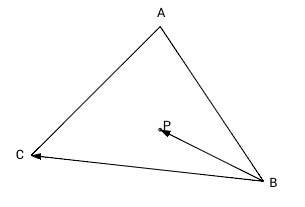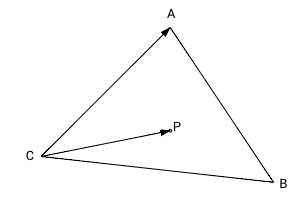
To determine if a point P is inside a triangle ABC, we compute 3 cross products: ABxAP, BCxBP, and CAxCP. Since we are in 2D space, the third vector coordinate (z) equals 0. According to the formula [1], we don't need to calculate the first two coordinates because the result x,y coordinate is always 0 because the z coordinate is 0 (the result vector is perpendicular to the ABC plane). The sign of remained (z) coordinate depends on the relative position of the vectors. If the first vector appears on the right of the second one, the z coordinate is positive; if the first vector appears on the left of the second one, the z coordinate is negative; otherwise (both vectors point to the same direction), the result is 0.
The remaining step to solving our problem is to analyze signs of the z coordinates. If we have both positive and negative results, then the point is outside the triangle; if we have only positive or only negative signs - the point is inside the triangle.
The following table illustrates all possible solutions.
| Drawing | Description |
|---|---|
  |
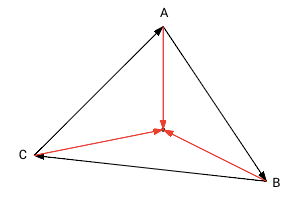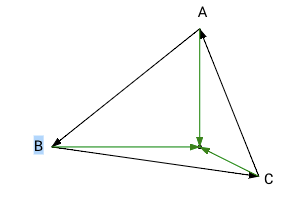All results are negative or positive. The point is inside the triangle. |
 |
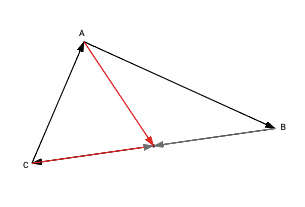One result is zero; the remaining ones are all positive or all negative. The point lies on the side of the triangle. If two results are zero, then the point coincides with a triangle vertex. |
 |
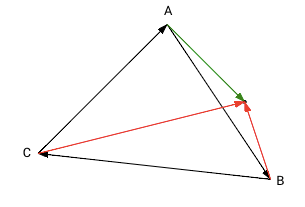We have both positive and negative results. The point is outside the triangle. |
Comments