Arc length calculator
This universal online calculator can find arc length of circular segment by radius and angle, by chord and height and by radius and height.
This page exists due to the efforts of the following people:
 | Timur
|
This content is licensed under Creative Commons Attribution/Share-Alike License 3.0 (Unported). That means you may freely redistribute or modify this content under the same license conditions and must attribute the original author by placing a hyperlink from your site to this work https://planetcalc.com/8336/. Also, please do not modify any references to the original work (if any) contained in this content.
This online calculator computes the arc length of a circular segment, given either the radius and angle of the segment, or the chord length and the height of the segment, or the radius and the height of the segment. The most useful thing, in my opinion, is the ability to find the arc length by the chord length and the height - these often can be measured directly (see the picture - the blue part is the circular segment, those arc length should be found).
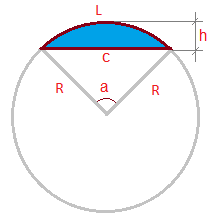
In the calculator below, choose the data you have to find the arc length, enter them and get the result. All formulas used for calculations are listed below the calculator.
Arc length calculator
Finding the arc length by the radius and the angle of the circular segment
The formula is simple:
Finding the arc length by the chord length and the height of the circular segment
Here you need to calculate the radius and the angle and then use the formula above.
The radius:
The angle:
Finding the arc length by the radius and the height of the circular segment
If you need to calculate the angle, then again use the formula.
The angle:
For universal calculator regarding circular segment in general, check out the Circular segment calculator. It finds chord length, segment height, segment perimeter, segment area, and arc length, depending on your data.
Comments