Spiral calculator
This online calculator computes unknown archimedean spiral dimensions from known dimensions. The spiral dimensions include: outer diameter, inner diameter, separation distance (distance between arms, thickness), spiral length, number of turnings
This is a universal calculator for the Archimedean spiral.

We have five spiral dimensions: outer diameter - D, inner diameter - d, thickness, separation distance or distance between arms - t, spiral length - L, number of turnings - n. These dimensions are related (see formulas below the calculator), and you can calculate any two if you know the other three.
We can see spirals in everyday life in any objects that are in the rolled form: rolls of paper, tapes, films, and so on. You can easily find out some of these objects' dimensions, like diameters and thickness, or a number of turnings, and, using the calculator below, calculate the missing ones. For example, you can calculate roll length from inner and outer diameters and roll thickness or number of turnings. You can also solve an inverse problem (when you know the roll length) - calculate thickness and number of turnings using roll length and both diameters. Theory and formulas, as usual, can be found below the calculator.
Please be careful with unit control when you enter the known dimensions! 20 meters are not the same as 20 millimeters...
Archimedean spiral
The Archimedean spiral (also known as the arithmetic spiral) is a spiral corresponding to the locations over time of a point M moving away from a center point O with a constant speed along a line OA that rotates around the center point O with constant angular velocity.

If we denote the distance from O to M as ρ, and rotation angle as φ, then we can describe a spiral with the polar equation:
,
where k is the size parameter, which equals to change of distance when the angle is rotated by 1 radian. After one turn (an angle increases by 2π), the distance increases by 2πk.
This increase is the distance between two arms of a spiral, separation distance, or spiral thickness. We can rewrite our initial equation using a:
Since thickness is constant, the more the point M moves away from the center, the more the spiral resembles the circle.
To derive the formula for the spiral length, we will examine infinitesimal length change.
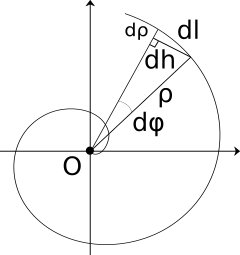
An infinitesimal spiral segment dl can be thought of as hypotenuse of the dl, dρ, and dh triangle. Hence:
An infinitesimal spiral segment dh can be replaced with an infinitesimal segment of a circle with radius ρ; hence its length is ρdφ.
Using the polar equation of a spiral, we can replace ρ with kφ, and dρ with kdφ
Now we have the dependence of the length dl on the angle dφ. To find out the length, we need to integrate from the initial angle to the final angle.
Long story short, the final integral is:
If a spiral starts from zero angle (from the center), the formula is simplified:
But in real life, of course, a roll of material does not start from the center. Usually, it has a sleeve, hence the inner diameter and initial angle. How are all these parameters related?
Here is how number of turns n is related to angles:
And here is how diameters are related to angles (this follows directly from the spiral polar equation)
These are all formulas that we need to find out unknown dimensions by known dimensions. However, note that the length equation is transcendental, and the inverse task (finding unknown dimensions while the length is among the known dimensions) requires numerical methods. This calculator uses Secant method.
Comments