Sexagesimal
Sexagesimal number converters. The calculator converts sexagesimal number to rational or decimal and vice versa.
This content is licensed under Creative Commons Attribution/Share-Alike License 3.0 (Unported). That means you may freely redistribute or modify this content under the same license conditions and must attribute the original author by placing a hyperlink from your site to this work https://planetcalc.com/9216/. Also, please do not modify any references to the original work (if any) contained in this content.
The sexagesimal numeral system is a base 60 numeral system, one of the oldest numeral systems invented by humanity. The system was initially introduced by the ancient Sumerians approximately in the 3rd millennium BC. People have been using the numeral system for millennia due to its merits.
Our calculator converts the input decimal or rational number to the sexagesimal form. The calculator has several types of output: the contemporary sexagesimal form; the cuneiform used in ancient Babylon; the medieval format; the mixed decimal-sexagesimal format.
You can use the following calculator to convert a sexagesimal number back to a rational (or decimal) number. The input is a number in any notation mentioned above. The cuneiform sexagesimal number can be entered using these symbols:
- < — for tens
- | — for units
- - — empty place, zero
- ; — fractional separator
- space — digit separator
Try the example
Sexagesimal numeral system history
There are currently many hypotheses about the predominance of the base 60 numeral system in Mesopotamia. One of the earliest belongs to Theon of Alexandria, who in the 4th century. AD suggested that the system was chosen because of its arithmetic properties, in particular, because the number 60 has the largest number of distinct divisors among small natural numbers 1: 1,2,3,4,5,6,10,12,15,20, 30.60
The mathematical writings of the ancient Babylonians, scribed in cuneiform on clay tablets, have been well preserved to this day.
At a certain point, the Babylonians came to a system of scribing all sexagesimal numbers using only 2 symbols:
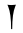
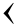
Combining these symbols, you can scribe a number from 1 to 59:

The ancient Babylonians had a positional numeral system for scribing large numbers, just like the contemporary decimal system. This means that the same symbols are used to scribe all the digits of a large number. Converting to a decimal number, the most significant digits must be multiplied by 60 to the power corresponding to the digit's position.
For example, a number < <| <<|| consists of 3 digits, from the lowest to the highest:
- cuneiform: <<|| decimal: 22 x 600
- cuneiform: <| decimal: 11 x 601
- cuneiform: < decimal: 10 x 602
Finally:
< <| <<|| = 10 x 3600 + 11 x 60 + 22 x 1 = 36 682.
In our calculator, a special symbol is used to fill in all zero cuneiform digits, including the least significant ones. But the ancient Babylonians did not know the zero symbol. An empty space indicated a place without value (zero value). Babylonians later devised a special sign to represent this empty place, but this sign did never appear in final (least significant) positions.
We also use a semicolon as a radix point, while the Babylonians did not use it at all. The position of the fractional digits could only be learned from the context.
After the Babylonians, ancient Greek astronomers, and the Middle Ages astronomers recorded their observations in sexagesimal form, paying tribute to the accuracy and compactness of fractional numbers representation. However, the decimal numeral system was also used in conjunction with the sexagesimal system. For example, in the Almagest of Ptolemy (2nd century AD), the measures of the angle are written in the form of a decimal integer part and a sexagesimal fraction 2. Our calculator also supports such a mixed numerals.
In medieval texts, the ambiguity of writing sexagesimal numbers is eliminated by using Arabic numerals, one or more accent marks to highlight the sexagesimal digit, and the decimal separator symbol (superscribed zero).
Example: 49‵‵‵‵36‵‵‵25‵‵15‵1°15′2″36‴49⁗ 3.
Since this accented format is completely unambiguous, you can safely skip empty digits. For example, our calculator recognizes the following sexagesimal number notation: 15‵2‴
The sexagesimal numeral system these days
The sexagesimal system is still successfully used today. For example, the number of minutes in one hour and seconds in a minute is 60. There are 60 arc-minutes in one degree and 60 arc-seconds in one minute.
Nowadays, we freely mix the sexagesimal system with the decimal system. It does not seem strange that we count minutes and seconds in the same way as the ancient people of Mesopotamia in the sexagesimal system, but the milliseconds are decimal. The calculator can recognize a colon-separated time interval with dot-separated milliseconds, for example: 1:48:10.250 (1 hour, 48 minutes, 10 seconds, 250 milliseconds). As a result, you get the total number of seconds.
The modern notation for sexagesimal numbers was suggested by Otto Neugebauer 4. He introduced the semicolon separator for a fractional part and the comma as an ordinary digit separator. For example, an approximation of the root of 2 will look like this: 1; 24,51,10
The calculator also accepts a mixed notation of a number with different separators and types of numbers (pseudo-cuneiform or Arabic numbers) in different digits.
Comments