Involute of an angle
Involute of an angle calculator and finding an angle by the given involute.
Plunging into the theme of gears and their calculations, I've encountered involute and evolvent terms. I thought that's interesting, and they deserve separate calculators, see them below. The first is for the involute, and two others are for finding the angle by the given involute. For those who are interested - the text about the involute is following the calculators.
So, in the differential geometry of curves evolvent is a curve, normal of which is tangent to the original curve at each point.
Because it's hard to grasp everything above, I'll retell you a figurative definition as it's described in the English version of the article (see. Involute on Wikipedia).
So, imagine a spool of thread, where the free end of the thread is lying on the spool. If you take this free end and start unwinding the thread while keeping it tight, the thread's end will describe some curve that will be an evolvent of the circle (spool is an original curve that is a circle).
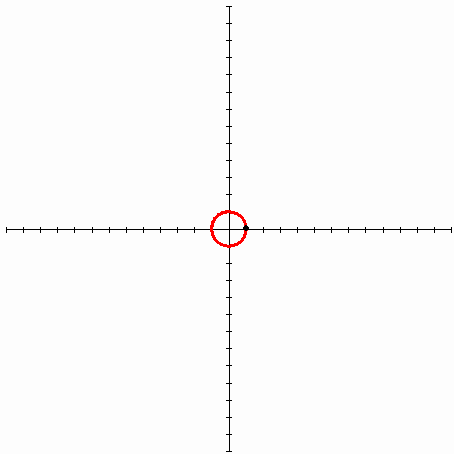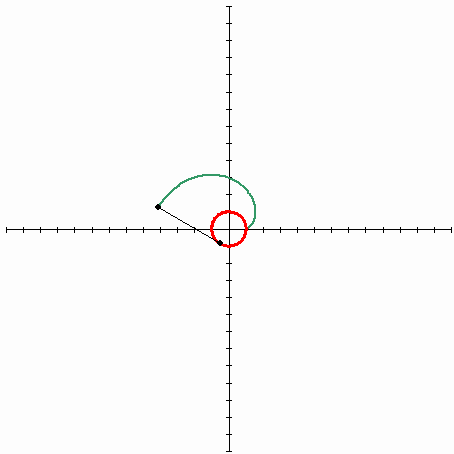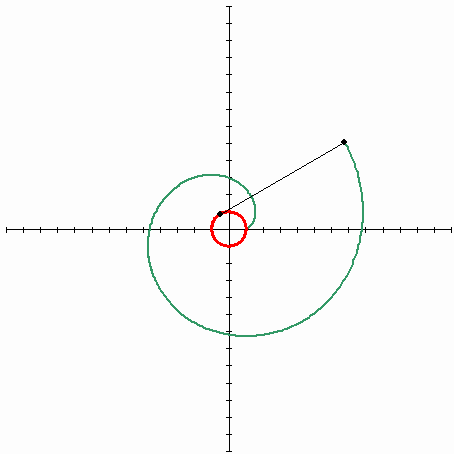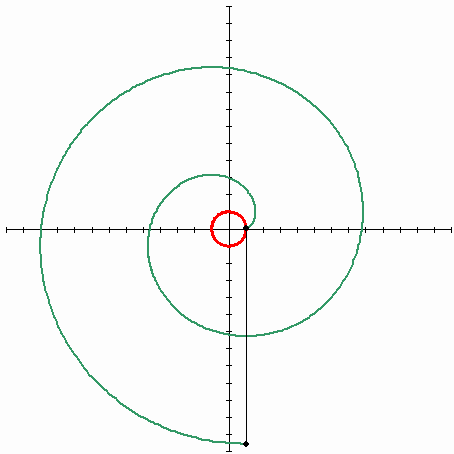
The following picture describes the evolvent of the circle
(Source - Wikipedia). The red line is an original curve(circle), the black line is a stretched thread, the green line is a trajectory of an end of the thread - the curve that is called the evolvent of the circle.
Speaking of involute, the term involute is used interchangeably with the term evolvent in English sources. So it can refer to the curve itself and its function. In the Russian sources, the term evolvent is used for a curve, and the term involute is for its function.
I think the term evolvent got much clearer for you after the picture above. Now, let's see what kind of function this is. The picture I've made will help:
The section at this picture equals the arc
(because this is our "thread"). Angle "φ" equals to the arc
that is called evolvent angle of roll and consist of a sum of "θ" angle (evolvent angle)"α" angle (angle of pressure). The arcs lenght is
Because is a right triangle that means
Equating these two arcs to each other, we will get, whence
This function
is called involute or the evolvent of the function.
The equations of involute curve in polar coordinates look like this
By the construction, we can see that the "α" angle can vary from 0 to 90 but excluding 90 because, in that case, straight-line KK will be parallel to MxN.
Why should we do all this? The evolvent of the circle is used in involute gearing - the gearing in which the profiles of the teeth have outlined the involute of the circle. During the involute gearing, common normal to the contact profiles' teeth always coincided with the common tangent to the base circle. This tangent is called the pressure line because the contact point of the teeth moves by that line during the wheel movement.
(картинка). This is the most common type of gearing.
And involute is used in calculations associated with involute gearing. Moreover, there are involute calculations and vice versa - finding an angle by its involute. And the second type of calculation is not that simple because the equation is a transcendental equation, and numerical methods can only solve it.
To sum up, we will review the numerical methods used in the calculators above - Laskin and Cheng methods (for more information see this)
Laskin's method
Based on Newton's method, which consists of an iterative calculation procedure
The Know-How of this thing is in the choice of the initial values, which by the method of Laskin is calculated as
, where I - initial value of the involute
To calculate the next approximation after the disclosure of derivative we'll obtain the expression
There are five iterations used in the calculator, but four should provide the accuracy to six decimal places. This method works for the values of involute from 0 to 1, i.e., you can find the angles from 0 to 64.87 degrees. In practice, that is enough. There are tables for finding the involute that are similar to the tables of trigonometric functions, and they have a range of angles from 0 to 60.
Cheng's method
Based on the determination of an approximate value using the asymptotic curves. Cheng brought the following formula:
You can use this method for finding the involute values that are strictly less than 1.8, i.e., it can find the angles up to 71.87. And you don't actually need those above - approaching the 90, the tangent tends to infinity, with all the ensuing consequences. Also, there are no tooth gearings with such large angles.
Comments