Volume of an elliptical paraboloid
This online calculator calculates the volume of an elliptical paraboloid by the height and length of the semi-axes (or radius in the case of a paraboloid of revolution).
This page exists due to the efforts of the following people:
 | Timur
|
This content is licensed under Creative Commons Attribution/Share-Alike License 3.0 (Unported). That means you may freely redistribute or modify this content under the same license conditions and must attribute the original author by placing a hyperlink from your site to this work https://planetcalc.com/9947/. Also, please do not modify any references to the original work (if any) contained in this content.
The formula for the calculation is listed below the calculator.
Volume of an elliptical paraboloid
Formula for the volume of an elliptical paraboloid
If we take a parabola, and start rotating it about its axis in three-dimensional space, we get a surface of rotation called a paraboloid of revolution. The cross section of the paraboloid of revolution with the horizontal plane (parallel to X and Y axes) with the equation z = h (h＞0) will form a circle. If the paraboloid of revolution is uniformly compressed/stretched, the cross section with a plane will form an ellipse, and the paraboloid itself will be called an elliptic paraboloid.
The volume of an elliptic paraboloid is the volume of the figure formed by the paraboloid and the plane perpendicular to the symmetry axis of the paraboloid. It is more correct, of course, to speak about the volume of a segment of the elliptic paraboloid. Such a figure will be characterized by the height H, as well as the lengths of the semi-axes of the ellipse formed by the section, a and b (see figure).
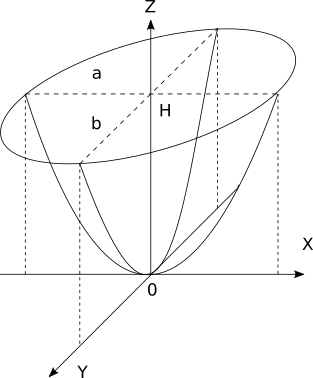
The formula for the volume of such a figure
In the case of a paraboloid of revolution, a = b = r and the formula equals
From the formula above, we can see that the volume of a segment of a paraboloid is half the volume of a cylinder with the same base and the same height. This result was obtained by Archimedes.
Comments