PLANETCALC Online calculators

Login
StudyMathGeometry

Cone

This page exists due to the efforts of the following people:

A

Anton

Timur

Timur

  • Article : Cone - Editor
Created: 2008-11-15 09:09:48, Last updated: 2021-03-05 16:50:19
Creative Commons Attribution/Share-Alike License 3.0 (Unported)

This content is licensed under Creative Commons Attribution/Share-Alike License 3.0 (Unported). That means you may freely redistribute or modify this content under the same license conditions and must attribute the original author by placing a hyperlink from your site to this work https://planetcalc.com/142/. Also, please do not modify any references to the original work (if any) contained in this content.

Cone is a three-dimensional figure that has one circular base and one vertex (apex).

Oblique cone
Oblique cone



Right cone
Right cone



An oblique cone is a cone with an apex that is not aligned above the center of the base.
A right cone is a cone in which the apex is aligned directly above the center of the base. The base need not be a circle here.

The volume of both right cone and oblique cone is V=\frac{1}{3}S_bH, where S_b is a surface area of cone base.

geometry_cone.gif

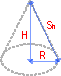
When the base of a right cone is a circle, it is called a right circular cone.
Such a cone is characterized by the radius of the base and the cone's altitude, that is, the distance from the vertex to the center of the base. So the volume of a circular cone is V=1/3\pi R^2H

The slant height of such a cone is the length of a straight line drawn from any point on the cone's perimeter to the vertex.
If the radius of the base is R and the altitude of the cone is H, then the slant height is H_s= \sqrt{R^2+H^2}
Now we can calculate total surface area of a right circular cone: S=S_{base} + S_{lateral}=\pi R^2 + \pi R H_s=\pi R^2 + \pi R \sqrt{R^2+H^2}

PLANETCALC, Cone

Cone

Digits after the decimal point: 5
Volume
 
Lateral surface area
 
Surface area
 



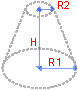
Right cone frustum scheme
Right cone frustum scheme



Right cone frustum
Right cone frustum



A frustum of cone is a truncated cone in which the plane cutting off the apex is parallel to the base.
Volume of a right circular cone frustum is V=\frac{1}{3}\pi (R_1^2+R_1 R_2 + R_2 ^2)H
Surface area of a right circular cone frustum is S=\pi R_1^2 + \pi R_2^2 + \pi (R_1+R_2)\sqrt{(R_1-R_2)^2 + H^2}

PLANETCALC, Cone frustum

Cone frustum

Digits after the decimal point: 5
Volume
 
Lateral surface area
 
Surface area
 

URL copied to clipboard

Similar calculators

 cone cone frustum Engineering calculators Geometry lateral surface area oblique cone right cone surface area volume
PLANETCALC, Cone
Anton2021-03-05 16:50:19

Comments