Cone
Cone is a three-dimensional figure that has one circular base and one vertex (apex).


An oblique cone is a cone with an apex that is not aligned above the center of the base.
A right cone is a cone in which the apex is aligned directly above the center of the base. The base need not be a circle here.
The volume of both right cone and oblique cone is , where
is a surface area of cone base.
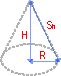
When the base of a right cone is a circle, it is called a right circular cone.
Such a cone is characterized by the radius of the base and the cone's altitude, that is, the distance from the vertex to the center of the base. So the volume of a circular cone is
The slant height of such a cone is the length of a straight line drawn from any point on the cone's perimeter to the vertex.
If the radius of the base is R and the altitude of the cone is H, then the slant height is
Now we can calculate total surface area of a right circular cone:
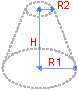

A frustum of cone is a truncated cone in which the plane cutting off the apex is parallel to the base.
Volume of a right circular cone frustum is
Surface area of a right circular cone frustum is
Comments