Circular segment
Here you can find the set of calculators related to circular segment: segment area calculator, arc length calculator, chord length calculator, height and perimeter of circular segment by radius and angle calculator.
This content is licensed under Creative Commons Attribution/Share-Alike License 3.0 (Unported). That means you may freely redistribute or modify this content under the same license conditions and must attribute the original author by placing a hyperlink from your site to this work https://planetcalc.com/1421/. Also, please do not modify any references to the original work (if any) contained in this content.
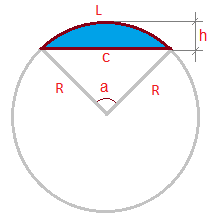
Circular segment - is an area of a "cut off" circle from the rest of the circle by a secant (chord).
On the picture:
L - arc length
h - height
c - chord
R - radius
a - angle
If you know the radius and the angle, you may use the following formulas to calculate the remaining segment values:
Circular segment formulas
Segment area:
[1]
Arc length:
Chord length:
Segment height:
If you don't know the radius and the angle, you can calculate the segment parameters by the chord length and the segment height:
The formula for the segment radius by the chord and the height:
Then, you can calculate the segment angle using the following formula:
You may also use the following calculator to obtain the segment area by its radius and height:
This calculator evaluates the angle by the following formula:
then it uses formula [1] to calculate the segment area.
15 circular segment calculations in one program
Finally, the circular segment calculator below includes all possible calculations regarding circular segment parameters:
- angle
- arc length
- area
- chord length
- height
- radius
Enter two segment parameters, and the calculator will find all the rest.
Comments