Pipe cold bending. Flexure depth with the main shaft.
Calculates the section flexure depth with pipe bender or bending machine to obtain given parameters.
This article was written by users' request to calculate the section flexure depth with the main shaft to obtain the bent pipe with given parameters.
Before the request, I didn't know that cold bending machines exist. Besides, there are industrial bending machines and manual hydraulic benders.
They are working the way you can see in the picture.
.

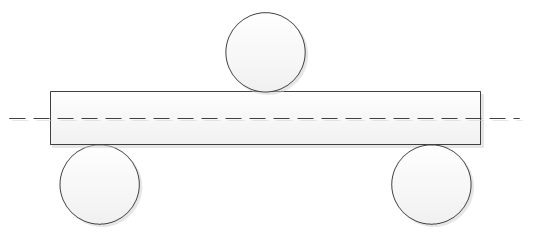
Section (pipe) is placed between the rollers, then the main roller bends the section, and the remaining part slides through the bending machine.
From my amateur point of view, this process looks like this
-
Placing the section
- Bending it
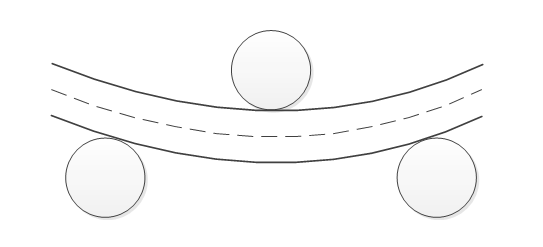
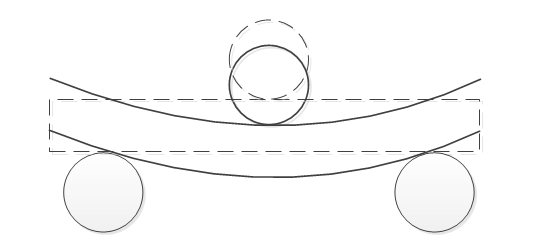
or, if we combine
So, the question is, how hard we should bend the tube, i.e., lower the main shaft that after sliding the section through, would we have the needed curve? The curve is set with a radius. But as the user's request showed, parameters can be set not by the radius only but by the length and height of a chord if you need an arc. The calculator that calculates the length of a section (L) and circle radius (R) by the given length (C) and chord height (h) - see the picture.
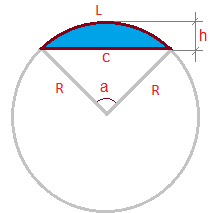
More info and formulas here- Circular segment
Let's move on.
If we need to have a flexure depth knowing the radius, distance between driven rollers, rollers radius, and section size.
Let's rewrite the combined picture, adding a few necessary lines and removing all unnecessary.
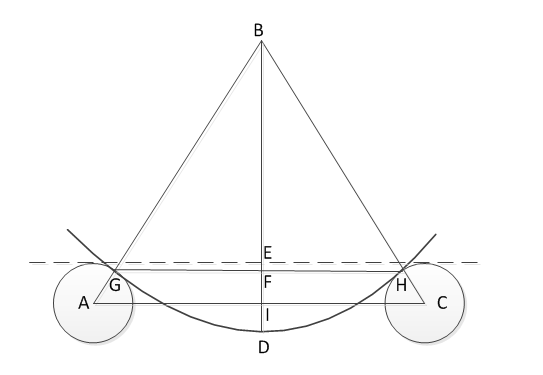
Point B is the center of our circle. Notice that the outer edge calculates the profile relative to the curve. Since the radius of the height and width of the chord is likely to be calculated according to the profile's axis, the radius of the profile should be added to the obtained radius so you will have the radius of the outer edge of the profile.
Then the geometry is used.
From the distance AC and AB we find ABD triangle
Hence
And here is the calculator
Comments