Regular polygon, number of sides and length of side from incircle and circumcircle radii
This online calculator finds number of sides and length of side of regular polygon given the radii of incircle and circumcircle
This page exists due to the efforts of the following people:
 | Timur
|
This content is licensed under Creative Commons Attribution/Share-Alike License 3.0 (Unported). That means you may freely redistribute or modify this content under the same license conditions and must attribute the original author by placing a hyperlink from your site to this work https://planetcalc.com/2823/. Also, please do not modify any references to the original work (if any) contained in this content.
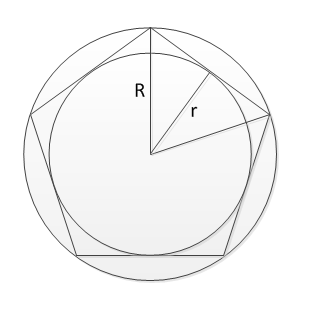
Well, I have to come back to incircles and circumcircles. I thought I've done with them after I've created Side length of the regular polygon to calculate length of polygon and Regular Polygon Incircle and Circumcircle Calculator to calculate radii, but I was wrong.
One of site visitors asked for "calculator which finds length of polygon side from incircle and circumcircle radii".
So, the problem is:
Some regular polygon has incircle with known radius and circumcircle with known radius. You need to find number of sides of this polygon and length of the side.
To make it clear, there is a picture on the left, presenting this situation.
If we look at triangle created by incircle radius r, circumcircle radius R and half side of regular polygon, we can see that there radii related by the formula
There alpha angle related to number of sides n of the polygon by the formula
Thus, known radii of incircle and circumcircle unambiguously define number of sides of the regular polygon by the formula
Finding the length of side is trivial.
Note about calculator - since we are talking irrational here (I mean there is irrational number pi in the formula) we can't expect to get integer result for number of sides. From we other side, we do know that number of sides is integer number. Thus, first this calculator calculates number of sides as is. Then result is rounded to the nearest integer. Then the length of side is computed using this integer, as well as incircle radius, the last one is for pure curiosity.
Comments