The length of arc of an Earth's parallel at a given latitude
This online calculator converts the arc length of an Earth's parallel at a given latitude from degrees to meters.
We have a calculator that calculates a meridian arc length as a function of latitude, more precisely, the length of the meridian arc of one minute, better known as a nautical mile. For completeness, I decided to write a calculator that calculates the size of the Earth's parallel arc length as a function of latitude. From fairly obvious considerations, the greater the latitude, that is, the closer we are to this or that pole, the smaller the size of the arc of, say, 1 degree in meters. Obviously, at the equator, the arc size would be the maximum (latitude is zero) and the one degree arc would be 111 km 319 meters (approximate). The calculator below calculates the size of the arc at a given latitude for the given arc's angular size. The formulas can be found below the calculator.
The length of the arc of an Earth's parallel
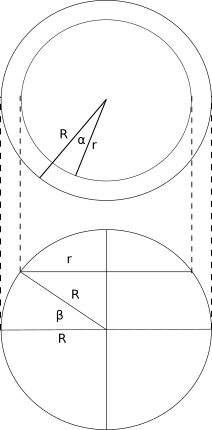
The calculation is quite simple, and is done from simple geometric considerations. We, of course, approximate the Earth as a sphere (although it is a geoid).
To find the arc length of a circle by the arc angle α, it is enough to multiply the radius of the circle r by the arc angle in radians
.
For an arc length of 360 degrees, or 2π radians, the formula transforms into the well-known formula for the length of a circle
As can be seen from the figure, at a certain latitude we are interested in the radius of the circle r obtained by cutting off a part of the sphere by a plane parallel to the plane of the equator. At the equator itself, the radius coincides with the radius of the earth R. Let us express the radius of interest through the radius of the Earth R and the given latitude β:
.
Accordingly, the final formula
And as the radius of the Earth we take the value defined in the standard WGS-84, namely, 6378137m. That's all.
Comments